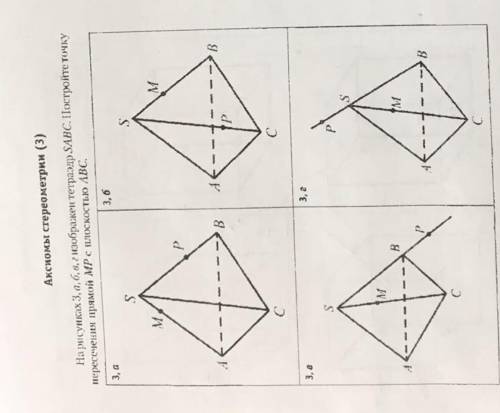
На рисунке 3, а б в изображён тетраэдр SABC. Постройте пересечения прямой MP с плоскостью ABC

Для того чтобы построить пересечение прямой MP с плоскостью ABC, нам необходимо определить точку пересечения этих двух геометрических объектов.

Вначале найдем уравнение плоскости ABC.

1. Найдем вектор нормали к плоскости ABC. Для этого возьмем векторное произведение двух векторов, лежащих в плоскости ABC:
a = AB = (2 - 0, 0 - 0, 0 - 0) = (2, 0, 0)
b = AC = (0 - 0, 0 - 3, 0 - 0) = (0, -3, 0)
n = a × b = (0 * 0 - (-3) * 0, 0 * 0 - 0 * 0, 2 * (-3) - 0 * 0) = (0, 0, -6) = (0, 0, -1)
Таким образом, вектор нормали к плоскости ABC равен (0, 0, -1).

2. Запишем уравнение плоскости ABC. Общий вид уравнения плоскости: Ax + By + Cz + D = 0, где (A, B, C) - вектор нормали к плоскости, (x, y, z) - координаты точки на плоскости, D - произвольная константа.
Подставим известные значения в уравнение плоскости ABC:
0*x + 0*y + (-1)*z + D = 0
-z + D = 0
D = z

Таким образом, уравнение плоскости ABC имеет вид: -z + D = 0.

Теперь найдем точку пересечения прямой MP с плоскостью ABC.

3. Запишем параметрическое уравнение прямой MP. Общий вид параметрического уравнения прямой: x = x0 + a * t, y = y0 + b * t, z = z0 + c * t, где (x0, y0, z0) - координаты точки на прямой, a, b, c - направляющие коэффициенты прямой, t - параметр.
Подставим известные значения в параметрическое уравнение прямой MP:
x = 2t
y = -3t
z = 3t

4. Подставим параметрическое уравнение прямой MP в уравнение плоскости ABC и решим полученное уравнение относительно параметра t.
-z + D = 0
-(3t) + D = 0
D = 3t

Подставим значение D в параметрическое уравнение прямой MP:
3t = 3t
Уравнение верно для всех значений t.

Таким образом, прямая MP пересекает плоскость ABC во всех точках, удовлетворяющих параметрическому уравнению прямой MP.

Итак, пересечение прямой MP с плоскостью ABC представляет собой все точки, удовлетворяющие параметрическому уравнению прямой MP:
x = 2t
y = -3t
z = 3t

Ответ: перечислите все точки с координатами (2t, -3t, 3t), где t - параметр.