1. Математика
  2. Сделайте Исследовать на экстремум

Сделайте Исследовать на экстремум функцию
y=x³+3x²

HELPPP11 HELPPP11    1   03.06.2020 21:25    1

Ответы
EvgenyMalkin71 EvgenyMalkin71  15.10.2020 12:59
1).

Для того, чтобы исследовать функцию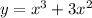 y=x^3+3x^2, найдем ее производную:

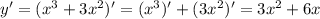
y' = (x^3+3x^2)' = (x^3)'+(3x^2)' = 3x^2+6x

2).

Приравняем производную к нулю и найдем абсциссы точек экстремума:

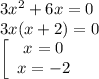
3x^2+6x=0\\3x(x+2)=0\\\left[\begin{array}{ccc}x=0\\x=-2\end{array}\right

3).

Исследуем знаки производной:

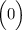+++++++++++++++\Big (-2 \Big)---------------\Big ( 0 \Big )++++++++++++++

Значит:

На промежутке ( - \infty; -2] функция возрастает.

На промежутке [-2;-1] функция убывает.

На промежутке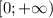 [0;+ \infty) функция возрастает.

4).

Найдем критические значения функции.

В точке максимума (x=-2):

y = x^3+3x^2 = (-2)^3+3 \cdot (-2)^2 = -8 + 12 = 4.

В точке минимума:

y = x^3+3x^2 = 0^3 + 3 \cdot 0^2 = 0.


Сделайте Исследовать на экстремум функцию y=x³+3x²
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
deloranka deloranka  14.07.2021 20:13
с первым и вторым или дать ссылку на ответы по тетради комбинированные летнии задания за 6 клас ​...
bondarevera bondarevera  14.07.2021 19:23
Обчисліть значення виразу3-³ × 9⁸ : 27⁵​...
selenagulya2002 selenagulya2002  14.07.2021 19:21
Подайте у вигляді степення вираз n3×(n2)6 И обьясните как вы посчитали? Я вот втыкаю втыкаю и не могу понять как решить....
arisazenina783 arisazenina783  14.07.2021 18:30
Решит это математические задачи​...
thewinterstale thewinterstale  14.07.2021 18:28
Не понял вот такую строчку - 1 000 000a + b делится на ab, следовательно, b делится на a . Объясните , откуда следует то, что b делится на a ЗадачаНайти два шестизначных...
Anway2017 Anway2017  14.07.2021 18:28
Яна обычно проплывает 1 км за 50 минут. Тренер посоветовал ей улучшить это время на 20%. На какой процент Яне следует увеличить скорость плавания для этого?...
СвежийГусь СвежийГусь  14.07.2021 18:28
В трикутник АВС вписано квадрат MLKN. Висота цього трикутника, проведена до сторони АС, дорівнює 6 см. Знайдіть периметр квадрата, якщо АС дорівнює 10 см.​...
taya99191 taya99191  14.07.2021 18:28
Знайти площу рівнобедреної трапеції, у якої довжини основ дорівнюють 10см і 26см, а діагоналі перпендикулярні до бічних сторін...
КаТюНя234556 КаТюНя234556  14.07.2021 18:28
Имеются 5 камней три одинаковых более легких и два одинаковых более тяжёлых Имеются чашечные весы без гирь сколько понадобится взвешиваний чтобы установить какие...
Vanea228 Vanea228  14.07.2021 17:14
Розв язати рівняння (x-1) (x-2)- x ^2=0...

Популярные вопросы