Найдите производные (с решением)
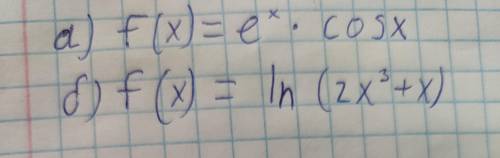
Другие вопросы по теме Математика
Популярные вопросы
- Один из углов треугольника равен 30° ,а противолежащая ему сторона...
2 - Прочтите отрывок из текста «Тихое утро» Ю.П.Казакова и дайте развёрнутый...
2 - Г) Найдите длину отрезка [ВС], если известно, что [АВ] = 7см, [АС]...
2 - с физикой Что из перечисленного НЕ является свойством электрического...
2 - Вагон массой 60т наталкивается на упор со скор. 0,2м / с .Оба буферные...
2 - Вы поймите что люди будут тупыми все до одного Вы хотите чтобы выхотите...
3 - во по физике Носителем малейшего положительного заряда является?...
3 - Записать правила речевого этикета при обращении со старшими...
2 - 1. Даны функции, найдите их производные. 2. а) х2 + 1/х3 3. б)х3+...
1 - Выполнить, используя цикл N раз. Не использовать команды покажись...
1
Пошаговое объяснение:
# a) f( x ) = eˣcosx ;
f '( x ) = ( eˣcosx )' = ( eˣ )'cosx + eˣ( cosx )' = eˣcosx - eˣsinx =
= eˣ( cosx - sinx ) ;
б ) f( x ) = ln( 2x³ + x ) ;
f '( x ) = [ ln( 2x³ + x ) ]' = 1/( 2x³ + x ) * ( 2x³ + x )' = ( 6x² + 1 )/( 2x³ + x ) .