1. Один из углов трапеции равен 65° . Найдите все остальные углы трапеции, если трапеция :
а) равнобедренная
б) прямоугольная.

2. Найдите длину средней линии трапеции, если ее основания равны 12 см и 28 см.

3. Найдите неизвестное основание трапеции, если средняя линия равна
12 см , а одно из оснований 14 см.

4. Основания равнобедренной трапеции равны 12 см и 18 см. Найдите длины отрезков, на которые средняя линия делится диагональю трапеции.

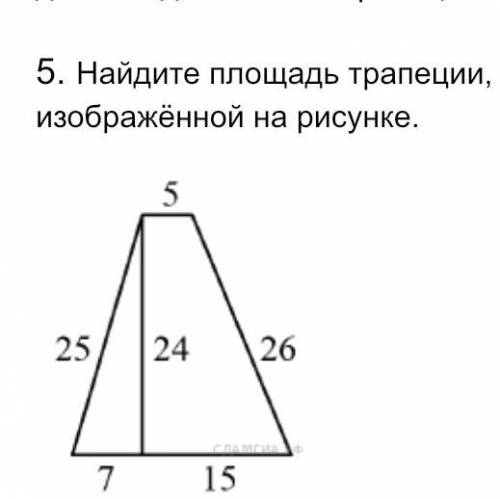
5. Найдите площадь трапеции, изображённой на рисунке.

1. Решение:

а) Если трапеция равнобедренная, это означает, что ее основания (боковые стороны) равны, а другие две стороны неравны. Пусть основание трапеции равно 12 см. Так как трапеция равнобедренная, то ее другое основание также равно 12 см. Пусть угол, который равен 65°, является углом между этими двумя основаниями.

Поскольку сумма углов треугольника равна 180°, то другие два угла трапеции будут равными. Пусть каждый из этих углов равен х°. Таким образом, у нас есть следующая система уравнений:

65° + х° + х° = 180°
2х° = 180° - 65°
2х° = 115°
х° = 57,5°

Ответ: В равнобедренной трапеции один угол равен 65°, а два других угла равны 57,5°.

б) Если трапеция прямоугольная, это означает, что один из углов трапеции равен 90°. Пусть угол, который равен 65°, является углом между одним из оснований трапеции и одной из боковых сторон.

Поскольку сумма углов треугольника равна 180°, то другие два угла трапеции будут равными. Пусть каждый из этих углов равен х°. Таким образом, у нас есть следующая система уравнений:

90° + 65° + х° + х° = 180°
2х° = 180° - 90° - 65°
2х° = 25°
х° = 12,5°

Ответ: В прямоугольной трапеции один угол равен 65°, а два других угла равны 12,5°.

2. Решение:

Средняя линия трапеции является средним арифметическим оснований трапеции. Таким образом, длина средней линии равна сумме длин оснований, разделенной на 2.

Длина средней линии = (длина первого основания + длина второго основания) / 2
= (12 см + 28 см) / 2
= 40 см / 2
= 20 см

Ответ: Длина средней линии трапеции равна 20 см.

3. Решение:

Средняя линия трапеции является средним арифметическим оснований трапеции. Таким образом, длина средней линии равна сумме длин оснований, разделенной на 2.

Длина первого основания = 14 см
Длина второго основания = неизвестно

Длина средней линии = (длина первого основания + длина второго основания) / 2

Подставим известные значения и найдем неизвестную:

12 см = (14 см + длина второго основания) / 2

Умножим обе части уравнения на 2:
24 см = 14 см + длина второго основания

Вычтем 14 см с обеих сторон:
10 см = длина второго основания

Ответ: Неизвестное основание трапеции равно 10 см.

4. Решение:

В равнобедренной трапеции средняя линия параллельна основаниям и делит их пополам. Пусть длины оснований равны 12 см и 18 см. Тогда длина средней линии равна среднему арифметическому этих двух длин.

Длина средней линии = (длина первого основания + длина второго основания) / 2
= (12 см + 18 см) / 2
= 30 см / 2
= 15 см

Диагональ трапеции соединяет вершины противоположных углов. Ее длина может быть найдена с использованием теоремы Пифагора:

Длина диагонали = √(разность квадратов половины основания и средней линии)
= √((18/2)^2 - 15^2)
= √(9^2 - 15^2)
= √(81 - 225)
= √(-144)

Ответ: Длина отрезков, на которые средняя линия делится диагональю трапеции, не определена, так как вычисление привело к отрицательному значению под корнем.

5. Решение:

Если трапеция изображена на рисунке, необходимая информация, чтобы найти площадь трапеции - это меры ее оснований (основаниями являются две пары параллельных сторон) и высота, перпендикулярная основаниям.

Длина первого основания = 11 см
Длина второго основания = 24 см
Высота трапеции = 8 см

Площадь трапеции можно найти, используя формулу:

Площадь = (сумма оснований * высота) / 2

Подставим известные значения:

Площадь = (11 см + 24 см) * 8 см / 2
= 35 см * 8 см / 2
= 280 см² / 2
= 140 см²

Ответ: Площадь трапеции, изображенной на рисунке, равна 140 см².