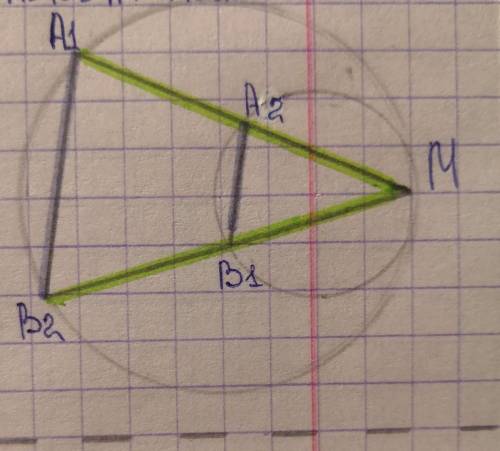
Докажите, что А1В2 и А2В1 параллельны.​

Две окружности касаются внутреннем образом в точке М. Через точку М проведены две прямые,  пересекающие одну окружность в точках А₁ , В₂ , а другую в точках А₂, В₁ . Докажите А₁В₂ ║А₂В₁

Объяснение:

Проведем  касательную МА . Она является касательной к обеим окружностям .

1) Для малой окружности . Угол ∠1 между касательной МА и хордой А₂М  , проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними : ∠1=1/2*∪А₂М

Вписанный угол ∠А₂В₁М=1/2*∪А₂М .Значит ∠1=∠А₂В₁М.

2) Для большей  окружности .Угол ∠1 между касательной МА  и хордой А₁М , проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними: ∠1=1/2*∪А₁М

Вписанный угол ∠А₁В₂М=1/2*∪А₁М. Значит ∠1=∠А₁В₂М .

3) Т.к. ∠1=∠А₂В₁М , ∠1=∠А₁В₂М  ⇒∠А₂В₁М=∠А₁В₂М .

Тогда по признаку параллельности прямых с соответственными углами , при секущей В₂М  ⇒ А₁В₂ ║А₂В₁