Необходимо решить систему уравнений. найти значение параметра, при котором нет решений, 1 решение, и x принадлежит r
$\left \{ {{ax+2y=a+2 \atop {2ax+(a+1)y=2a+4}} \right.$

Ответы

1DiamonDragon1 10.10.2020 07:14

$\left \{ {{ax+2y=a+2 \atop {2ax+(a+1)y=2a+4}} \right.$

приведем оба уравнения системы к виду y=kx+b(уравнение прямой).

$1)\ ax+2y=a+2\\2y=a-ax+2\\2y=-a*x+a+2\\y=-\frac{a}{2}*x+\frac{a+2}{2} \\2)\ 2ax+(a+1)y=2a+4\\2ax+ay+y=2a+4\\y(a+1)=-2ax+2a+4\\y=-\frac{2a}{a+1} *x+\frac{2a+4}{a+1}$

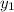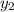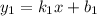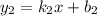Если две прямые y_1 и y_2 заданы уравнениями y_1=k_1x+b_1 и y_2=k_2x+b_2 , то на плоскости они могут быть:

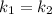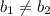1) k_1=k_2 и $b_1\neq b_2$ - прямые параллельны, следовательно они не пересекаются и, следовательно, система из таких прямых не имеет решений.

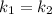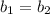2) k_1=k_2 и b_1=b_2 - прямые совпадают, следовательно, система из таких прямых будет иметь бесконечное множество решений.

3)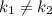 $k_1\neq k_2$ - прямые пересекаются в одной точке, следовательно, система из таких прямых будет иметь только одно решение.

Применим это для решения данной задачи:

$y_1=-\frac{a}{2}*x+\frac{a+2}{2}\\k_1=-\frac{a}{2};\ b_1=\frac{a+2}{2}\\y_2=-\frac{2a}{a+1} *x+\frac{2a+4}{a+1}\\k_2=-\frac{2a}{a+1};\ b_2=\frac{2a+4}{a+1}\\$

$1)\left \{ {{k_1=k_2} \atop {b_1\neq b_2}} \right. \Rightarrow \left \{ {{-\frac{a}{2}=-\frac{2a}{a+1}} \atop {\frac{a+2}{2}\neq \frac{2a+4}{a+1}}} \right. \Rightarrow \left \{ {{-a^2-a=-4a} \atop {a^2+2a+a+2\neq 4a+8}} \right. \Rightarrow \left \{ {{a^2-3a=0} \atop {a^2-a-6\neq 0}} \right. \\a^2-3a=0\\a(a-3)=0\\a_1=0;\ a_2=3\\a^2-a-6=0\\D=1+24=25=5^2\\ a_{3,4}=\frac{1\pm 5}{2} =3;\ -2$

$\left \{ {{\left[ \begin{array}{cc}a=0\\a=3\end{array}\right. } \atop {\left[ \begin{array}{cc}a\neq 3\\a\neq -2\end{array}\right.}} \right. \Rightarrow a=0$

Значит, при a=0 данная система не имеет решений.

$2)\left \{ {{k_1=k_2} \atop {b_1= b_2}} \right. \Rightarrow \left \{ {{-\frac{a}{2}=-\frac{2a}{a+1}} \atop {\frac{a+2}{2}= \frac{2a+4}{a+1}}} \right. \Rightarrow \left \{ {{-a^2-a=-4a} \atop {a^2+2a+a+2= 4a+8}} \right. \Rightarrow \left \{ {{a^2-3a=0} \atop {a^2-a-6= 0}} \right.\\\left \{ {{a^2-3a=0} \atop {a^2-a-6= 0}} \right.\\a^2-3a=0\\a(a-3)=0\\a_1=0;\ a_2=3\\a^2-a-6=0\\D=1+24=25=5^2\\ a_{3,4}=\frac{1\pm 5}{2} =3;\ -2\\a_2=a_3\Rightarrow a=3$