Диагональ BD параллелограмма ABCD перпендикулярна стороне AB и равна 16 cm. Вычислите длины сторон параллелограмма, если угол BDA равен 30°.
ответы должны быть:
см.фото
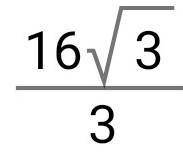
Другие вопросы по теме Геометрия
Популярные вопросы
- Answer the questions. Write complete sentences.How do you think Bob felt...
2 - Написать 8- 10 предложений делового стиля из какой-либо книги указать...
3 - ~ , ~, и ~ Придумать предложения по схеме с профессиональными словами...
2 - Каковы были географические познания европейцев в Средине века ? Откуда...
2 - B=42см и это 7/15 от AC - составляет - 5/6 от AКакой объем прямоугольного...
1 - Как решить эти примеры. Тема: Применение производной. Класс 10-11 распишите...
1 - Определите стиль речи данного текста. Обоснуйте свою точку зрения. Какие...
1 - При делении какого числа на 19 остаток равен 4 ? a)1030b)1111c)952d)879e)...
2 - сделать таблицу по истории 7 класс ...
2 - Контрольная работа по грамматике 10 класс...
1
Первым шагом решения будет определение длины стороны AB. Так как диагональ BD перпендикулярна стороне AB, то сторона AB будет являться высотой треугольника ABD, а сторона BD - основанием этого треугольника.
Мы знаем, что в треугольнике ABD высота (сторона AB) разбивает основание (сторона BD) на две равные части. С учетом этого, мы можем рассматривать треугольник ABD как равнобедренный треугольник.
Зная угол BDA, который равен 30°, мы можем найти угол DAB, так как сумма углов треугольника равна 180°. Так как у треугольника ABD два равных угла (закон равности оснований), то угол DAB будет равен (180° - 30°)/2 = 75°.
Теперь мы можем использовать тригонометрические отношения в равнобедренном треугольнике ABD, чтобы найти длину стороны AB. Рассмотрим синус угла DAB:
sin(75°) = сторона AB / сторона BD.
Мы знаем, что сторона BD равна 16 см, и можем использовать эту информацию для нахождения стороны AB:
16 см * sin(75°) = сторона AB.
Выполнив этот расчет, получим:
16 см * 0.9659 ≈ 15.45 см.
Таким образом, длина стороны AB приближенно равна 15.45 см.
Далее, чтобы найти длину стороны AD, мы можем использовать синус угла BDA, так как у нас есть длина диагонали BD:
sin(30°) = сторона AD / сторона BD.
Подставив известные значения:
sin(30°) = сторона AD / 16 см.
Решим эту пропорцию:
0.5 = сторона AD / 16 см.
Теперь найдем длину стороны AD:
0.5 * 16 см = сторона AD.
Это приводит нас к ответу:
8 см = сторона AD.
Таким образом, длина стороны AD равна 8 см.
Итак, для данного параллелограмма сторона AB ≈ 15.45 см, сторона AD = 8 см, сторона BC = 16 см, и сторона CD ≈ 15.45 см.