Если ребро куба увеличить в 4 раза то Как изменится объём куба и площадь его основания

LilyBlackk 3 24.10.2021 23:29 98

Question

Алгебра: Если ребро куба увеличить в 4 раза то Как изменится объём куба и площадь его основания

LilyBlackk · Answer

Пусть ребро куба равно а .

Тогда его объём равен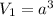 V_1=a^3 , площадь основания равна S_1=a^2 .

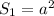Теперь ребро стало равно 4а .

И объём куба с таким ребром равен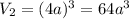 V_2=(4a)^3=64a^3 , а площадь

основания равна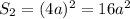 S_2=(4a)^2=16a^2 .

$\dfrac{V_2}{V_1}=\dfrac{64a^3}{a^3}=64\ \ ,\ \ \ \dfrac{S_2}{S_1}=\dfrac{16a^2}{a^2}=16$

Объём увеличился в 64=4³ раз , а площадь увеличилась в 16=4² раз .

Если ребро куба увеличить в 4 раза то Как изменится объём куба и площадь его основания