1. Алгебра
  2. Дослідити функцію диференціального

Дослідити функцію диференціального числення та використовуючи результати досджень,побудувати її графік надо

PrivPomogite PrivPomogite    3   22.05.2019 12:40    0

Ответы
1972jkmxbr 1972jkmxbr  17.06.2020 23:10

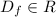
οбласть :  D_f \in R

 

первая производная :

 

\frac d{dx} f(x)= \frac d{dx}\frac{1}{6}x^3-\frac d{dx}x^2+\frac d{dx}1= \frac{1}{6}\cdot 3x^2-2x+0=\frac{x^2}{2}-2x

 

второя производная :

 

\frac{d^2 } {dx} f(x) = \frac d {dx} (\frac{x^2}{2}-2x)= \frac d {dx} \frac{x^2}{2}-\frac d {dx}2x)= \frac 1 2 \cdot 2x -2= x-2

 

принципя

 

1. f(x) возрастающая  если  производная > 0

2. f(x) убывающая если  производная < 0

3. f(x) неубывающая  и невозрастающая (стала или екстремум ) если  производная = 0

 

4. f(x) вypuкла если  второя производная > 0

5. f(x) вогнутая если  второя производная < 0

6. f(x) невypuкла и невогнутая  ( перегиб или прямая ) если  второя производная = 0

 

ад 3

 

екстрема

 

\frac{x^2}{2}-2x = 0 \newline \newline \frac x 2(x -4) = 0                   x_1= 0 \newline \newline x_2 = 4

 

f(0) = \frac{1}{6} \cdot 0^3-0^2+1= 1

f(4) = \frac{1}{6} \cdot 4^3-4^2+1= -\frac{13}{3}

 

ад 1

 

возрастание

 

\frac{x^2}{2}-2x 0 \newline \newline \frac x 2(x -4) 0                       \left \{ {{x<0} \atop {x4}} \right

 

ад 2

 

убывание

 

\frac{x^2}{2}-2x < 0 \newline \newline \frac x 2(x -4) < 0                         0<x<4

 

 

ad 6

 

перегиб

 

x-2 =0 \newline \newline x=2

 

f(2) = \frac{1}{6} \cdot 2^3-2^2+1= -\frac{5}{3}

 

 

ad 4

 выпукла:

 

x-2 0 \newline \newline x 2

 

ад 5

 

вогнутая

 

x-2 < 0 \newline \newline x <2

 

 тепер рисуем  : во вложению  граф

 

 

 

 

 


Дослідити функцію диференціального числення та використовуючи результати досджень,побудувати її граф
ПОКАЗАТЬ ОТВЕТЫ
silwana2002 silwana2002  17.06.2020 23:10

y'=0.5x²-2x

0.5x²-2x=0

x(0.5x-2)=0

x=0 или 0.5x-2=0

             0.5x=2

               x=4

-----+--------0------------4-------+------>

(-∞;0)∨(4;∞) возрастает

(0;4) убывает

х=0 точка max (0;1)

х=4 точка min   (4; -4,3333)


Дослідити функцію диференціального числення та використовуючи результати досджень,побудувати її граф
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
BitBul1 BitBul1  03.06.2019 08:30
Решить систему уравнений: система: х-2у=4 ху=6...
Aleksiy69 Aleksiy69  03.06.2019 08:30
Точки а и б имеют координаты а(5; -2), б(-2; 3) найти отрезок аб...
liza2002623 liza2002623  03.06.2019 08:30
Скільки треба змішати 50 відсоткового розчину і35 відсоткового розчину сірчаної кислоти щоб одержати 500 гр 40 відсоткового розчину?...
sholpsholp3owhb3d sholpsholp3owhb3d  03.06.2019 08:30
Вокружности провели хорды ab и cd, которые перпендикулярны друг другу и пересекаются в точке p так, что ap =39,bp =9,cp =13,dp=27. найдите радиус окружности. ответ : 25...
maZIK007 maZIK007  03.06.2019 08:30
Запишите уравнения прямой в виде y=kx+l и назовите коэффициенты k и l: а) х+у=5; б) 2х+у=-3; в) 3х-2у=6; г)10х+100у=200...
Кети20060106 Кети20060106  03.06.2019 08:30
Оцените периметр и площадь прямоугольника со сторонами c см и b см, если известно что 4,6...
krashakova krashakova  23.06.2019 08:50
Найти площадь фигуры,ограниченной параболой y=x^2-4 и прямой y=2x-1....
alikhan12 alikhan12  23.06.2019 08:50
4x⁴-17x²+4=0 рациональное уравнение...
polinavorkuta polinavorkuta  23.06.2019 08:50
Докажите тригонометрическое тождество. sin(30+x)*cosx-cos(30+x)*sinx=0,5...
arinaschool1 arinaschool1  23.06.2019 08:50
Найдите значение выражения (3sin(а+2п)-2cos(п/2+а))/2sin(а-2п)...

Популярные вопросы