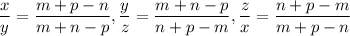В треугольник, длины сторон которого относятся как m : n : p, вписан круг. Найти отношение, в котором каждая точка касания делит
соответствующую сторону треугольника.
Другие вопросы по теме Математика
Популярные вопросы
- Заттың формуласы:CuCl2; Na2S;FeO:Заттың мөлшері:3 моль;? ;? Массасы:?...
2 - 1. Определите, где содержится больше атомов. ответ обоснуйте. [Впишите...
3 - для детского сада купили 120 плюшевых игрушек каждая игрушка получила...
2 - Вставьте пропущенные слова. Все предложение переписывать не нужно,только...
2 - Тест по технологии 6 класс Вырезаемые участки размечают знаком:...
3 - Сравни дробь: а) 3 1/2 и 2 17/20б)5/101 и 5/17в)7/9 и 5/6...
2 - Луч MP является биссектрисой угла CMB. Точки B и C соединены отрезками...
2 - Кто такой Будда?Назовите основные положения его учения...
3 - В Древней Индии индуизм доминировал над буддизмом? Расположи события...
1 - Упражнения для разных мышц построить мост из существующей позиции...
2
Пошаговое объяснение:
Введём следующие обозначения. Обозначим вершины треугольника как A, B, C, причём AB : BC : AC = m : n : p. Обозначим точки касания с AB как M, с BC — N, AC — P, отрезки касательных AM = AP = x, BM = BN = y, CN = CP = z (отрезки касательных, проведённых из одной точки, равны).
Из отношения AB : BC : AC = m : n : p следует, что AB = mk, BC = nk, AC = pk. Тогда получаем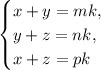
Вычтем из третьего уравнения второе и запишем его в системе с первым: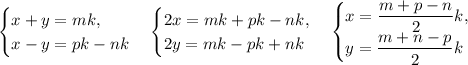
Подставим найденный x в третье уравнение и выразим z: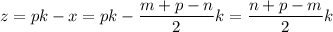 .
.
Тогда искомые отношения: