Теория вероятностей в связке имеются 5 различных ключей , из которых только одним ключом можно отпереть дверь. наудачу выбирается ключ и делается попытка

Question

Математика: Теория вероятностей в связке имеются 5 различных ключей , из которых только одним ключом можно отпереть дверь. наудачу выбирается ключ и делается попытка открыть дверь. ключ, оказавшийся подходящим, больше не используется. найдите вероятность того, что для отпирания двери будет использовано не более двух ключей

MadPrinter · Answer

X — для отпирания двери будет использован - ый ключ.

Вероятность того, что для отпирания двери будет использован первый ключ, равна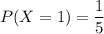 $P(X=1)=\dfrac{1}{5}$ , а второй ключ - 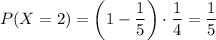$P(X=2)=\left(1-\dfrac{1}{5}\right)\cdot\dfrac{1}{4}=\dfrac{1}{5}$ (здесь первый множитель - вероятность того, что ключ не подойдет для отпирания двери, тогда остается 4 ключа из которых вероятность взять ключ для отпирания двери равна 1/4 ). По теореме сложения, вероятность того, что для отпирания двери будет использовано не более двух ключей равна

$P(X\leq2)=P(X=1)+P(X=2)=\dfrac{1}{5}+\dfrac{1}{5}=\dfrac{2}{5}=0.4$

Популярные вопросы