решить интеграл 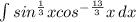 . ответ должен получиться:
. ответ должен получиться: 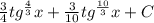
Другие вопросы по теме Математика
Популярные вопросы
- Решить с объяснением. самое главное объясните и почему) , ! завтра контроша(...
1 - 15 ) заранее ! найдите площадь треугольника со сторонами 10, 24, 26...
3 - Ыз жібек» жырытақырыбы мен идеясыкейіпкерлер әлемікөркемдік ерекшеліктері...
1 - Уменьши величины в 4 раза 8 ч 8 дм 2 ч 6 дм 2 сут 2 дм 1 мин 1 дм...
1 - ~ ходить, ходить зима гаэм - бiлоснiжна, килимочки простеляэ по дорiжках....
2 - Информацию про жибек жолы на казахском языке...
1 - Напишите письмо-обращение от лица анары к родителям. 10 ....
1 - Пересекаются ли две плоскости в одной точке...
3 - На ярмарке сладости участвуют 50 каждый день происходит ровно одно из...
3 - Даны вершины четырёхугольника а(1; -3; 2), в(1; 4; 0), с(-4; 1; 1) и д(-5;...
2
Пошаговое объяснение: