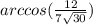Даны вершины четырёхугольника а(1; -3; 2), в(1; 4; 0), с(-4; 1; 1) и д(-5; -5; 3) найти углы между ac и bc
Другие вопросы по теме Математика
Популярные вопросы
- 1)собственная память человека,2) внешняя память,3) любой материальный объект...
1 - Меняя форму слова,составьте и запишите предложения-загадки. 1.над,повиснуть,крашеный,река,коромысло.(радуга)...
2 - Придумать текст на тему огород 3 класс...
1 - 5,3умножить на 10в квадрате плюс 0,37умножить на 10 в кубе...
1 - Укажите, в каком предложении из произведений а.с. пушкина выделенное слово...
1 - Спиши устно поставь слово в форму множественного числа.выдели окончание.подчеркни...
1 - Выделенные слова измените так чтобы в них появилось сочетание чк че, кормить...
1 - 29 + 7 х( х - 4)=54 решить уравнение...
2 - Спишите, заменяя данные приставки другими так, чтобы в словах образовались...
3 - Опилите на ураинском свою комноту с обоями где что стоит сильно надо...
1
Пошаговое объяснение:
AC = (-4 - 1; 1 - (-3); 1 - 2) = (-5; 4; -1)
BC = (-4 - 1; 1 - 4; 1 - 0) = (-5; -3; 1)
∠(AC; BC) =