1. Математика
  2. Поясните решение почему

Поясните решение почему ответ 9,если у меня в Задание пишут найдите корень уравнения √27+6x=x. Если уравнение имеет более одного корня, укажите меньший из них.

КсюшаКотW КсюшаКотW    3   05.05.2020 17:50    2

Ответы
Dushanbe2003 Dushanbe2003  18.08.2020 12:53

Возведем уравнение в квадрат (обе части), это можно сделать лишь при условии x≥0. То есть x<0 не годится.

27+6x = x^2

x^2 - 6x - 27 = 0

D = 6² + 4·27 = 36 + 80 +28 = 36 + 108 = 144 = 12²,

x = \frac{6\pm12}{2} = 3\pm6

x_1 = 3-6 = -3

x_2 = 3+6 = 9.

Делаем проверку x₁, подставляем в исходное уравнение и получаем

левая часть =

=\sqrt{27+6\cdot(-3)} = \sqrt{27 - 18} = \sqrt{9} = 3

правая часть = -3 ≠ левой части. x₁ не годен.

Проверка x₂, подставляем

левая часть =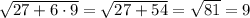 \sqrt{27 + 6\cdot9}=\sqrt{27+54} = \sqrt{81} = 9

правая часть = 9.

ответ. 9.

ПОКАЗАТЬ ОТВЕТЫ
JeDor15 JeDor15  18.08.2020 12:53

Решите уравнение.

\sqrt{27+6x} = x

- - - - - - - - -

\sqrt{27+6x} = x

Возведём обе части уравнения в квадрат, чтобы избавиться от знака корня в левой части.

{(\sqrt{27+6x})}^{2} = {x}^{2} \\\\ 27+6x = {x}^{2}

Перенесём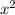 x^2 в левую часть уравнения с противоположным знаком.

27+6x-x^2=0

Меняем слагаемые в левой части местами.

-x^2+6x+27=0

Домножаем обе части уравнения на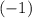 (-1).

x^2 - 6x - 27 = 0

Вычисляем дискриминант.

D = b^2 - 4\cdot a \cdot c = (-6)^2 - 4\cdot 1 \cdot (-27) = 36 +108 = 144 = 12^2

Находим корни уравнения.

x_{1,2} = \frac{6\pm 12}{2} \\\\ x_1 = \frac{6- 12}{2} = \frac{-6}{2} = -3 \\\\ x_2 = \frac{6+ 12}{2} = \frac{18}{2} = 9

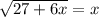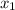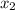Получили, что у уравнения \sqrt{27+6x} = x есть 2 корня. Но не стоит спешить. Давайте попробуем подставить значения x_1 и x_2 в уравнение, и проверим, подходят ли корни.

1. \; \; \sqrt{27+6x} = x \\\\ x = 9 \rightarrow \sqrt{27+6 \cdot 9} = 9 \\\\ \sqrt{81} = 9 \Rightarrow 9=9

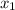Верно! x_1 подходит.

2. \; \; \sqrt{27+6x} = x \\\\ x = -3 \rightarrow \sqrt{27+6 \cdot (-3)} = -3 \\\\ \sqrt{9} = -3 \Rightarrow 3 = -3

ЛОЖЬ! Этот корень не подходит. Он посторонний. Значит уравнение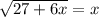 \sqrt{27+6x} = x имеет 1 корень. Он равен 9.

ОТВЕТ: 9.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
gaziza4 gaziza4  08.06.2019 20:50
Как решить уравнения ? как решить уравнения ? =( 1/21y-1/3y1/14y=5/14 9,6-(2,6-y)=4 4,2+(x-5,8)=2,5 0,7x-0,4x-0,96x=12,73...
yashchenko04 yashchenko04  08.06.2019 20:50
Найдите корень уравнения 0,72÷(0.8-x)=1.5...
baby2525 baby2525  08.06.2019 20:50
Найдите значение выражения 0,5х^2-10.6, при х=-4...
маріна2017 маріна2017  08.06.2019 20:50
Найдите уравнение касательной к графику функции f(x) = -x^2 - 4x +2 в точке с абсциссой х0=-1...
Veranda11 Veranda11  08.06.2019 20:50
Иван отправился в гости к другу, который назвал ему номер дома, подъезда и квартиры, но ничего не сказал про этаж. друг ивана живет в девятиэтажном доме в квартире № 86. подходя...
makhero111 makhero111  08.06.2019 20:50
Пешеход рассчитал, что двигаясь с определённой скоростью, намеченный путь он пройдёт за 2,5 часа. но он шёл со скоростью, превышающей намеченную на 1 км\ч, поэтому путь за 2 часа....
Maxutka007 Maxutka007  08.06.2019 20:50
Втрёхэтажном доме жильцов в 11 разв трёхэтажном доме жильцов в 11 раз меньше чем в девятиэтажном.сколько жильцов в девятиэтажном доме,если в трёхэтажном живёт 63 человека? заполни...
Asa77 Asa77  08.06.2019 20:50
Скорость лодки против течения реки 0,9 км/ч. собственная скорость лодки 3,2 км/ч. найдите скорость течения реки и скорость катера по течению....
Kotbarsikrulit Kotbarsikrulit  08.06.2019 20:50
С: в одном ящике было в 5 раз больше апельсинов,чем в другом.после того , как из первого ящика взяли 16 апельсинов,а во второй положили 12 апельсинов,апельсинов в ящиках стало...
larry19 larry19  08.06.2019 20:50
Два парохода вышли из порта,следуя один на север , другой на запад. скорости их равны соответственно 15 км/ч и 20 км/ч. какое расстояние в (километрах будет между ними через 2...

Популярные вопросы