Определить тип дифференциального уравнения первого порядка и найти его общее решение:
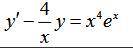
Другие вопросы по теме Математика
Популярные вопросы
- На научную конференцию приехали ученые из нескольких университетов. на церемонии...
1 - Сколько страниц в рассказе чехова шуточка...
2 - Длина одного катета прямоугольного треугольника на 4 см больше, чем длина другого...
1 - Log2(7-×)=5 как правильно его рассписать...
2 - Краткое содержание марк твен том сойер 5 глава...
1 - Сколько граммов уксусного альдегида можно получить из 44,8 л ацетилена н.у в реакции...
1 - Сколько литров воды нужно для 20 кг льда?...
1 - Расположите страны в порядке убывания естественного прироста населения а) нигерия...
3 - Чем отличается этилен от двинила ? а)по гибридному состояниб атомов углерода b)...
3 - Напишите краткий и понятный пересказ : ,,барышня-крестьянка . краткий, но ясный...
1
Это линейное ДУ
Замена:
общее решение