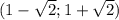Обчислити проміжки зростання та спадання функції f(x)=x^3-3x^2-3x+2
Другие вопросы по теме Математика
Популярные вопросы
- Как сделать синтаксический разбор предложения синтаксический разбор ссп: резкий...
3 - напишите сочинение-рассуждение.объясните,как вы понимаете смысл финала текста:...
1 - C5h10o2 класс органических соединений...
3 - :в первый день тракторист вспахал 14 1\2 га. во второй день 13 3\4 га, в третий...
2 - Два куска проволки длиной 70 и 182 см надо разрезать так чтобы не было отходов....
3 - Одну сторону квадрата уменьшили на 20%, а другую-увеличили на 20%.как и на...
3 - Сформируйте двухмерный массив и удалите из него все строки в которых встречается...
3 - Яка маса натрій гідроксиду міститься в 0,1 м розчині naoh об ємом 500 мл...
2 - Классификация, свойства нерастворимых оснований, получение, применение на...
1 - Underline the correct verb form in each sentence. a) can i have another book?...
2
Похідна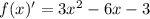
Прирівнюємо похідну до нуля та знаходимо нулі функції
При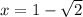 похідна міняє знак з (+) на (-) , це точка максимуму. Таким чином,
похідна міняє знак з (+) на (-) , це точка максимуму. Таким чином, 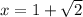 - точка мінімуму.
- точка мінімуму.
Проміжки зростання:
Проміжки спадання: