Найти точки экстремума функции (x^3 + 27) / (3x - x^2) С подробным решением
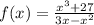
Другие вопросы по теме Математика
Популярные вопросы
- Первый кусок проволоки на 54 длинее второго от каждого куска отрезали...
2 - Что нужно сделать, чтобы не задохнуться в снежной траншее и других...
1 - Вкажіть функцію глікокаліксу: а) синтез білків; в) міжклітинна взаємодія;...
1 - На яблоне выросло 36 яблок, а на груше 12. во сколько раз яблок...
2 - Начертить два разных прямоугольника с периметром 14 см. это за 4...
3 - Между двумя металлическими пластинами, расположенными горизонтально...
1 - Cократите дробь [tex]\frac{2a^4+3a^3+2a+3}{(a^2-a+1)(2a+3)}[/tex]...
2 - Запиши числовые выражения.найди значения выражений...
3 - Write a letter to an english-speaking friend. • ask your friend...
3 - Что обозначает воля птички дороже золотой клетки...
2
Берем производную, приравниваем к нулю
Производная = 3х^2-6x-9=0
Решаем уравнение
Д=36+3*4*9=144
х12=(6+-12)/6= -1 и 3
При х=0, производная = -9 (отрицательная, т. е фенкция убывает в этой области) , т. е. точки
При х=-1, у=-3 - максимум
При х=3, у=-35 - минимум
Пошаговое объяснение:
Посчитаем производную
Найдем её нули
Решим первое:
Ни один из этих корней не противоречит предыдущему условию. Значит мы нашли точки экстремума!