1. Математика
  2. Найти общее решение дифференциального

Найти общее решение дифференциального уравнения 2xy'''=y''

vage205 vage205    3   24.06.2020 00:49    0

Ответы
Катрин703 Катрин703  15.10.2020 14:47

Пошаговое объяснение:

Обозначим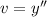  v = y'', после подстановки в уравнение, получаем:

2xv'= v

2x\frac{dv}{dx} = v

\frac{dv}{v} = \frac{dx}{2x}

Интегрируя, получаем

\log(v) = \frac{\log(x)}{2} + C

теперь берем экспоненту от обеих  частей:

v = C\sqrt{x}

(константа уже другая)

y = \int \int v = \int \int C\sqrt{x} dxdx= \int C_1x^{\frac{3}{2}} + C_2dx = C_1x^{\frac{5}{2}} + C_2 x+C_3

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
sofiko07161 sofiko07161  17.09.2019 17:30
Решите уравнением. в двух камандах 315 спортсменов.в первой в 2 раза больше чем во 2. сколько спортсменов в первой команде? пусть во второй команде было х спортсмкнов тогда...
Dmitry0232141 Dmitry0232141  17.09.2019 17:30
Впассажирском поезде 14 вагонов сколькими можно распределить по вагонам 14 проводников если за каждым вагоном закреплен один проводник сколько углов меньших 360 градусов получится...
DanaCorgi DanaCorgi  17.09.2019 17:30
Дана треугольная призма в основание,которой лежит треугольник abc,с углом с =90 градусов ас=15 см,вс=20см и высота 12 см.найти площадь боковую и площадь полной поверхности...
додо7 додо7  17.09.2019 17:30
Вычеслите 2) минус одинацать трицетьшесых разделить минус две целых три четвертых...
DarinaKim1 DarinaKim1  17.09.2019 17:30
Пассажир имеет движущуюся силу до 2 км/ч со скоростью 80км/ч .чтобы добраться до пункты назначения,необхадима принят в 4 раза менше чем текучий..сколько км до города...
shkolnik1233 shkolnik1233  17.09.2019 17:30
Найдите корень уравнения: 1) 3(x-2)=x+2 2) 5-2(x-1)=4-x 3) (7x++3)=5 4) 3,4+2y=7(y-2,3) 5) 0,2(7-2y) =2,3-0,3(y-6) заранее !...
taske047Ataske taske047Ataske  17.09.2019 17:30
Найдите неизвестный член пропорции x: 12=18: 24 25: 5=20: x x: 7=7: 1 20: x=64: 16 8: 32=x: 24 8: 4=x: 8...
даня1166 даня1166  17.09.2019 17:30
(4 сут. 6 ч 15 мин - 18 ч 29 мин + 5 сут. 12 ч 14 мин) : 9 = только ответ....
мартина мартина  17.09.2019 17:30
Найди все натуральные значения x при которых дробь x /15 будет правильной...
mila320 mila320  17.09.2019 17:30
Решите уравнение : е) - 2 3/8+d=3/5 з) t+3/25=3,7 к) 13/)=-2,3....

Популярные вопросы