1. Математика
  2. Найти наибольшее и наименьшее

Найти наибольшее и наименьшее значение функции на промежутке [0;π/2]


Найти наибольшее и наименьшее значение функции на промежутке [0;π/2]

Маринетт1210 Маринетт1210    1   05.12.2020 23:43    0

Ответы
olya2399 olya2399  04.01.2021 23:44

Наибольшее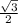 \frac{\sqrt{3}}{2}

Наименьшее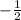 -\frac{1}{2}

Пошаговое объяснение:

Наибольшее значение функция принимает в правой границе отрезка - при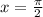 x=\frac{\pi}{2}:

y(\frac{\pi }{2} )=sin(\frac{\pi }{2} -\frac{\pi }{6} )=sin\frac{\pi }{3} =\frac{\sqrt{3} }{2}

Наименьшее значение функция принимает в левой границе промежутка - при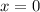 x=0:

y(0)=sin(0-\frac{\pi }{6})=sin(-\frac{\pi }{6} )=-\frac{1}{2}

ПОКАЗАТЬ ОТВЕТЫ
smail520 smail520  04.01.2021 23:44

Наименьшее значение функции на промежутке [0;π/2]: -0,5

Наибольшее значение функции на промежутке [0;π/2]: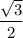 \displaystyle \frac{\sqrt{3}}{2}

Пошаговое объяснение:

Видно, что наименьшее значение этой функции на промежутке [0;π/2] находится в точке с аргументом "0"

Если подставить значение аргумента "0" в формулу графика то мы получим значение: sin(-π/6)=-0,5

Это и есть наименьшее значение функции на промежутке [0;π/2].

Также видно, что наибольшее значение функции на промежутке [0;π/2] находится в точке с аргументом "π/2"

Поставим в формулу вместо "х" чтобы найти значение функции при значении аргумента "π/2"

\displaystyle sin \left( \frac{\pi}{2} - \frac{\pi}{6} \right) = sin \left( \frac{3\pi - \pi}{6} \right) = sin \left(\frac{2\pi}{6} \right) = sin \left( \frac{\pi}{3} \right) = \frac{ \sqrt{3} }{2}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Kat11166 Kat11166  05.11.2020 14:48
Какой предмет следующий? Скриншот рисунка во вложении...
Raz1elGG Raz1elGG  05.11.2020 14:48
Із 7 кг зібраних маслюків отримали 5 кг почищених. Скільки кілограмів мас- люків потрібно, щоб отримати 40 кг почищених? 4000 кг почищених?​...
Abdulmansur Abdulmansur  05.11.2020 14:48
Даны множества А и В: A = {3;6;7;10}, B = {2;3;10;12}. Найти: А∪В,А∩В,А\В,А∆В....
allahakbar1062p0a3z0 allahakbar1062p0a3z0  05.11.2020 14:48
1)12-y=5(4-2y)+102)2-2(x-8)=4x-4 распишите всё...
66666666ak 66666666ak  05.11.2020 14:48
Который дробь будет равняться дробy 1/2...
mgvzvit2005 mgvzvit2005  05.11.2020 14:48
Найдите производные следующих функций...
Snowghost Snowghost  05.11.2020 14:48
Найти неопределённые интегралы...
FayaKuraeva FayaKuraeva  05.11.2020 14:48
Тест по теме «Свойства функций»hello_html_m5adce43b.png Указать область определения функции, заданной графиком: 1) (2;4) 2) [-4;2] 3) (-1;3] 4) [-4;4) Найти точку...
leonidkhadzhinov leonidkhadzhinov  05.11.2020 14:48
Алет решил 240 задач. 7/12 задач решил дома остальное в школе. что больше? количества решённых задач в школе или количества решённых задач дома...
vbratilova4 vbratilova4  05.11.2020 14:47
На автогонках при заезде на первой автомашине вероятность победить , при заезде на второй автомашине . Найти: вероятность того, что победят обе автомашины; вероятность...

Популярные вопросы