1. Математика
  2. Найдите значение наименьшего

Найдите значение наименьшего члена последовательности, которая задана формулой n-ого члена: an=n^2+(16/n)

nata121114 nata121114    3   01.10.2019 01:20    1

Ответы
CISA9999 CISA9999  09.10.2020 06:58

Найдём производную функции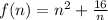 f(n)=n^2+\frac{16}{n}

f'(n)=2n-\frac{16}{n^2}=\frac{2n^3}{n^2}

2n^3-16=0\Rightarrow n=2

Найдём знаки производной:

    -         -           +

--------о--------*---------->

        0         2             n

То есть точка минимума функции n = 2. Значит, наименьший член последовательности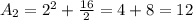 A_{2}=2^2+\frac{16}{2}=4+8=12

ответ: 12

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Nadin18 Nadin18  09.05.2020 13:20
Найдите все такие значения параметра a, при каждом из которых уравнение 2x^3+(3a+2)*x^2+ax-3a^2=0 имеет ровно два различных действительных корня...
SvetLink SvetLink  09.05.2020 13:20
У двох коробках разом 24 олівці.У першій корбці їх на 6.На скільки олівців менше в першій коробці,ніж у дрцгій?...
стас489 стас489  09.05.2020 13:20
4. Найти решение задачи Коши y +(3x^2 y)/(x^3+1)=(1+x^3 ) y^2 sin⁡(x) , y(0)=1 . 5. Указать, в каком виде необходимо искать частное решение неоднородного уравнения y″-6y +9y=x...
берик7 берик7  09.05.2020 13:20
Номер 1427 2 решите подстановки...
1saridua1 1saridua1  09.05.2020 13:20
1. Найти общее решение дифференциального уравнения xy^ -y=x sin^2(⁡y/x). 2. Найти общее решение дифференциального уравнения y^ -y ctgx=sin⁡x/x. 3. Найти общее решение дифференциального...
6666628 6666628  09.05.2020 13:20
Знайти другий, шостий і сотий члени послідовності (Вn), заданої формулою n-го члена Вn= n²-10n (дуже...
LizaVeta281 LizaVeta281  04.10.2019 19:20
Какое натуральное число лежит между числами пи и е?...
mainura2006 mainura2006  04.10.2019 19:20
Испытание нового прибора началось в 7 часов 30 минут и закончилось только на следующих день в 17 часов.сколько часов длилось испытание?...
элюсся5 элюсся5  04.10.2019 19:20
Вновогоднем подарке по 10 ирисок ,карамелек,батончиков и леденцов.через дырочку мышке удалось достать 6 конфет . вероятность того,что среди них есть хотя бы две ириски...
ещКеРе11 ещКеРе11  04.10.2019 19:20
Вычеслите площядь круга диаметр которого равен 1) 18см 2)3,6м...

Популярные вопросы