Найдите решения уравнения sin x = √2/2 удовлетворяющие условию cos x меньше 0 (обратите внимание что уравнение без минуса)
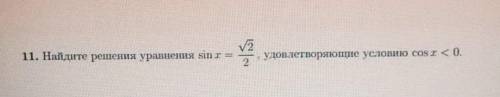
Другие вопросы по теме Математика
Популярные вопросы
- Що символізує квітка неопалимої купини? Як про це сказано в легенді?...
2 - Що є незвичним у розказаній історії? Що могло відбуватися насправді, а що...
1 - Що народ хотів сказати цим твором? Прочитай речення, у якому висловлено головну...
3 - Чи схожа ця легенда на казку? Підтвердь свою думку...
2 - Що змусило ворогів відступити від міста без бою?...
2 - Що народ хотів сказати цією легендою?...
1 - Чому легенду названо саме так? Чи можна дати їй іншу назву?...
3 - У тексті знайди ключові слова, які дають уяву про місце події. Спираючись...
3 - Розташуй у правильній послідовності істот, з якими пес хотів товаришувати...
2 - Що є правдивим, а що незвичним у розказаній історії?...
1
Значение sin x = √2/2 соответствует двум углам: 45 градусов и 135 градусов. Это можно определить, зная значения основных тригонометрических функций на основных углах (0, 30, 45, 60, 90 градусов).
Теперь обратим внимание на условие cos x < 0. Значение cos x меньше 0 на углах между 90 и 180 градусами.
Таким образом, нам нужно найти значения угла x, которые соответствуют sin x = √2/2 и cos x < 0.
Угол 45 градусов удовлетворяет условию cos x < 0, поскольку в первом квадранте (0-90 градусов) значение cos x всегда положительно.
Угол 135 градусов также удовлетворяет условию cos x < 0, так как он находится в третьем квадранте (90-180 градусов), где значение cos x отрицательно.
Таким образом, решения уравнения sin x = √2/2 при условии cos x < 0: x = 45 градусов и x = 135 градусов.
Пояснение:
Углы 45 градусов и 135 градусов определяются по основным тригонометрическим значениям sin и cos на основных углах. В первом квадранте (0-90 градусов) значения sin x и cos x положительны. Во втором квадранте (90-180 градусов) sin x положительно, а cos x отрицательно. В третьем квадранте (180-270 градусов) значения sin x и cos x отрицательны. В четвертом квадранте (270-360 градусов) sin x отрицательно, а cos x положительно. Поэтому, чтобы найти угол x, удовлетворяющий условию sin x = √2/2 и cos x < 0, мы ограничиваем поиск во втором и третьем квадрантах.