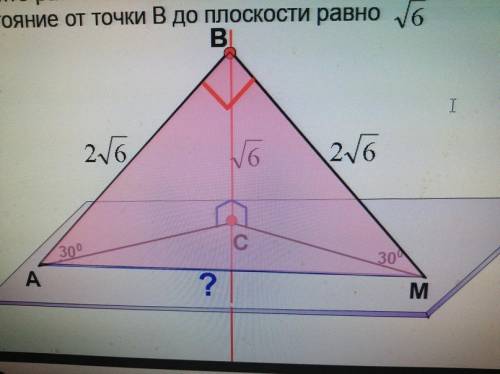
Из точки В к плоскости проведены две

наклонные, которые образуют со своими проекциями на

плоскость углы в 300. Угол между наклонными равен 900.

Найдите расстояние между основаниями наклонных, если

расстояние от точки В до плоскости равно корень из 6

Для решения данной задачи, нам понадобятся следующие шаги:

Шаг 1: Вспомним определение угла между двумя наклонными нитями. Угол между двумя наклонными нитями это угол между их проекциями на плоскость. В данном случае, у нас дан угол между наклонными нитями равный 900.

Шаг 2: Формируем уравнение для нахождения длины основания наклонных. Обозначим одно основание как x, а другое как y. Таким образом, мы сталкиваемся с прямоугольным треугольником, где сторонами являются основания наклонных нитей, а гипотенузой - расстояние между ними. Можем использовать следующее уравнение:

x^2 + y^2 = (корень из 6)^2 = 6

Шаг 3: Воспользуемся геометрическим свойством треугольников, согласно которому сумма углов треугольника равна 1800. Поскольку угол между наклонными нитями составляет 900, а угол между проекциями нитей на плоскость равен 300, можем утверждать, что угол между проекциями на плоскость каждой из нитей составляет r = 1800 - 900 - 300 = 600.

Шаг 4: Для нахождения длины основания, используем тригонометрические функции. Обозначим длину одной из наклонных нитей как l. Тогда мы можем применить следующее уравнение:

cos(r) = x / l

Выражая x через l, имеем:

x = l * cos(r)

Шаг 5: Решим уравнение, соединяющее основания наклонных нитей. Заметим, что в нашем случае, основания нитей равны и обозначим их как d. Таким образом, можем записать:

x = y = d

Соединяя все полученные уравнения, имеем:

d^2 + d^2 = 6

2d^2 = 6

d^2 = 3

d = корень из 3

Ответ: Расстояние между основаниями наклонных нитей составляет корень из 3.