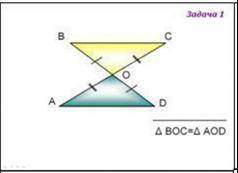
Доказать равенство треугольников AOD и BOC, если известно, что AO=OC и BO = OD.

Для доказательства равенства треугольников AOD и BOC мы можем использовать постулат равенства двух треугольников, а именно, две фигуры равны, если все их соответствующие стороны и углы равны.

Дано:
AO=OC и BO=OD

Необходимо доказать равенство треугольников AOD и BOC.

Для начала, давайте обратим внимание на стороны треугольников AOD и BOC.

У нас есть AO=OC, что значит, что стороны AO и OC равны.

Также, у нас есть BO=OD, что значит, что стороны BO и OD равны.

По свойству равных сторон треугольников, мы можем сказать, что треугольники AOD и BOC имеют две равные стороны, и это уже дает нам основание предположить, что треугольники могут быть равными.

Однако, нам также необходимо доказать равенство углов треугольников AOD и BOC.

Обратимся к изображению.

Мы видим, что угол AOD и угол BOC образованы одними и теми же сторонами: AO и OD (OC).

Так как мы уже знаем, что стороны AO и OC равны, то их углы (угол AOD и угол BOC) также будут равны, поскольку они образованы равными сторонами.

Таким образом, треугольники AOD и BOC имеют две равные стороны и один равный угол, что соответствует условию постулата равенства двух треугольников.

Следовательно, мы можем сделать вывод о равенстве треугольников AOD и BOC (AOD≡BOC).