1. Даны матрицы А = 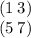
В =
Выяснить, какие из следующих операций можно выполнить:
1) A+ B; 2) A' + В; 3) A+ В'; 4) АВ; 5) ВА; 6) A'B; 7) АВ'; 8) A'B';
9) В'А'.
с разъяснениями
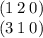
Другие вопросы по теме Математика
Популярные вопросы
- 1. 1целая 13/15•5/8•2 целых 2/7= 2. 2целых 1/4•16/27•4 целых 1/3=...
2 - Найдите наименьший корень уравнения |3x²-3x+5|=|2x²+6x-3|...
1 - Какой объем при н.у. занимает 20 г водорода (h2)...
1 - Сделать план жизни на 1 год ( по месяцам )...
1 - Что умеют делать белые медведи // ответьте побыстрее...
2 - На тело действуют 2 силы: f1 и f2.определите модуль и направление равнодействующей...
3 - Решить уравнение log5(x^2-8)=log5 2x...
3 - Примеры счастья в художественной ? пояснить ответ...
2 - Як називають активну частину м яза ?...
2 - Что общего в строении покровных ткани растений и животных...
3
1) A + B
Для сложения матриц необходимо, чтобы они имели одинаковый размер. Матрица A имеет размер 2x2, а матрица B имеет размер 2x3. Таким образом, операцию сложения невозможно выполнить.
2) A' + B
A' обозначает транспонированную матрицу A. Для транспонирования матрицы меняются ее строки и столбцы местами.
Транспонированная матрица A будет иметь размер 2x2:
A' =
Теперь попробуем выполнить операцию сложения:
A' + B =
Сложение двух матриц происходит поэлементно. То есть, складываем элементы матрицы A' и B с одинаковыми индексами:
Таким образом, операцию A' + B можно выполнить, и результатом будет матрица размером 2x3.
3) A + B'
B' обозначает транспонированную матрицу B. Транспонированная матрица B будет иметь размер 3x2:
B' =
Попробуем выполнить операцию сложения:
A + B' =
Операция сложения невозможна, так как матрицы имеют разный размер. Матрица A имеет размер 2x2, а матрица B' имеет размер 3x2.
4) AB
Для перемножения матриц необходимо, чтобы количество столбцов первой матрицы было равно количеству строк второй матрицы. Матрица A имеет размер 2x2, а матрица B имеет размер 2x3. Так как количество столбцов матрицы A не равно количеству строк матрицы B, операцию умножения выполнить невозможно.
5) BA
Для перемножения матриц необходимо, чтобы количество столбцов первой матрицы было равно количеству строк второй матрицы. Матрица B имеет размер 2x3, а матрица A имеет размер 2x2. Так как количество столбцов матрицы B не равно количеству строк матрицы A, операцию умножения выполнить невозможно.
6) A'B
A' обозначает транспонированную матрицу A. Транспонированная матрица A будет иметь размер 2x2:
A' =
Попробуем выполнить операцию умножения:
A'B =
Умножение матриц происходит путем умножения элементов строк первой матрицы на соответствующие элементы столбцов второй матрицы и суммирования произведений.
Таким образом, операцию A'B можно выполнить, и результатом будет матрица размером 2x3.
7) AB'
B' обозначает транспонированную матрицу B. Транспонированная матрица B будет иметь размер 3x2:
B' =
Попробуем выполнить операцию умножения:
AB' =
Операция умножения невозможна, так как матрицы имеют разный размер. Матрица A имеет размер 2x2, а матрица B' имеет размер 3x2.
8) A'B'
A' обозначает транспонированную матрицу A. Транспонированная матрица A будет иметь размер 2x2:
A' =
B' обозначает транспонированную матрицу B. Транспонированная матрица B будет иметь размер 3x2:
B' =
Попробуем выполнить операцию умножения:
A'B' =
Операция умножения будет выполняться аналогично пункту 6, но с учетом того, что обе матрицы уже транспонированы.
Таким образом, операцию A'B' можно выполнить, и результатом будет матрица размером 2x3.
9) B'A'
A' обозначает транспонированную матрицу A. Транспонированная матрица A будет иметь размер 2x2:
A' =
B' обозначает транспонированную матрицу B. Транспонированная матрица B будет иметь размер 3x2:
B' =
Попробуем выполнить операцию умножения:
B'A' =
Умножение матриц будет выполняться по тем же правилам, что и в пункте 6, но с учетом того, что порядок перемножения матриц изменен.
Таким образом, операцию B'A' можно выполнить, и результатом будет матрица размером 3x2.
Итак, из всех предложенных операций можно выполнить следующие:
2) A' + B
6) A'B
8) A'B'
9) B'A'
Для всех остальных операций невозможно выполнение, так как матрицы имеют разные размеры или не выполняются правила перемножения матриц.