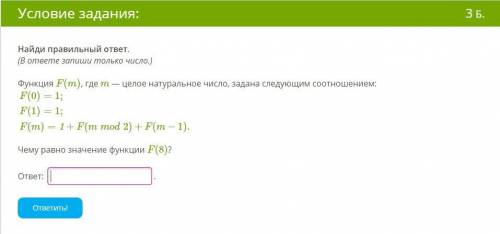
Найди правильный ответ. (В ответе запиши только число.)
Функция F(m), где m — целое натуральное число, задана следующим соотношением:
F(0)=1;F(1)=1;F(m)=1+F(mmod2)+F(m−1).
Чему равно значение функции F(8)?
Можно с объяснением плз
Другие вопросы по теме Информатика
Популярные вопросы
- Почему цинк по сравнению с медью хорошо растворяется в серной кислоте?...
1 - Что угол PLN равен углу PNL известно MN = LK и LM = KN Вставьте пропуски!...
2 - Заранее !! 1.три проявления нравственной ответственности ученых...
2 - Самый распространённый жанр музыкально-литературного творчества: Выберите...
3 - Растения водоема А)тимофеевка, пастушья сумка, нивяник Б)брусника, черника,...
3 - Треугольник стороны которого равны a=15, b=12, c=13 доказать что треугольник...
3 - запишите только ответ Task 1 - Fill in the sentences with the correct form...
1 - На координатной плоскости отметьте точки со следующими координатами, соединяя...
1 - 3.3. Проверьте правильность написания следующих слов. Слов...образование,...
2 - 1.Practice the new words. Вставьте пропущенные буквы. Напишите слова. r…ver,...
3
3628
Объяснение:
Значение функции равно , 257, исходя из формул
Первым шагом в соотношении заданы значения функции F(0) и F(1):
F(0) = 1,
F(1) = 1.
Далее, соотношение говорит нам, что значение F(m) равно сумме трех выражений:
F(m) = 1 + F(m mod 2) + F(m - 1).
Теперь приступим к нахождению значения F(2). В соответствии с соотношением:
F(2) = 1 + F(2 mod 2) + F(2 - 1) = 1 + F(0) + F(1) = 1 + 1 + 1 = 3.
При нахождении значения F(3):
F(3) = 1 + F(3 mod 2) + F(3 - 1) = 1 + F(1) + F(2) = 1 + 1 + 3 = 5.
Продолжим:
F(4) = 1 + F(4 mod 2) + F(4 - 1) = 1 + F(0) + F(3) = 1 + 1 + 5 = 7.
F(5) = 1 + F(5 mod 2) + F(5 - 1) = 1 + F(1) + F(4) = 1 + 1 + 7 = 9.
F(6) = 1 + F(6 mod 2) + F(6 - 1) = 1 + F(0) + F(5) = 1 + 1 + 9 = 11.
F(7) = 1 + F(7 mod 2) + F(7 - 1) = 1 + F(1) + F(6) = 1 + 1 + 11 = 13.
Наконец, находим F(8):
F(8) = 1 + F(8 mod 2) + F(8 - 1) = 1 + F(0) + F(7) = 1 + 1 + 13 = 15.
Таким образом, значение функции F(8) равно 15.