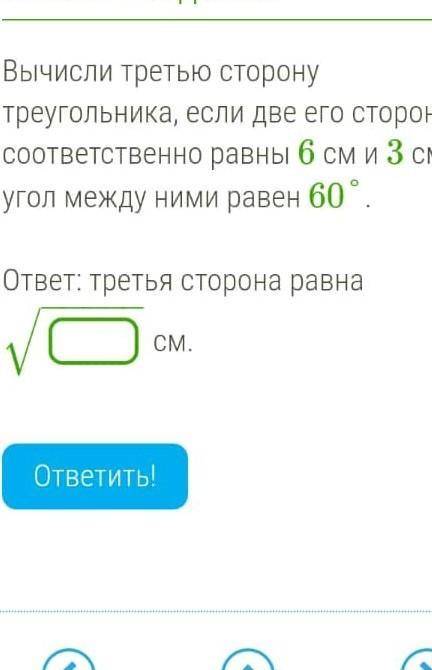
Вычисли третью сторону треугольника, если две его стороны соответственно равны 2 см и 9 см, а угол между ними равен 60°.
Другие вопросы по теме Геометрия
Популярные вопросы
- ГАР/ГОР Возг_раемостьвыг_раниевыг_ретьг_рючийг_релкадог_раниедог_рающийдог_ревзаг_релыйзаг_раниеизг_ратьнаг_ратьнаг_ревшийнаг_реть...
2 - 788 разделить в столбик с проверкой...
3 - Сделать плакат на тему космос с пк или телефона...
2 - Определи почему так называли эти предметы людей явления...
2 - Рабочий катит тележку массой 600 кг со скоростью 9км/ч . Определите...
3 - Підібрати коефіцієнти до схем хімічних реакцій Ca+ O2 + CaOHgO...
2 - Синквейн Роза 1два прилагательных 2 три глагола З предложение...
3 - Можете скорее решить верхнее задание, это сольфеджио 3 класс...
2 - Какая величина называется постоянной?...
1 - Термоядерна реакція це реакція......
1
У нас есть треугольник с двумя известными сторонами, которые равны 2 см и 9 см, и также углом между ними, который равен 60°.
Для начала, давайте обратимся к теореме косинусов, которая поможет нам вычислить третью сторону треугольника. Она гласит:
c^2 = a^2 + b^2 - 2ab*cos(C),
где c - третья сторона треугольника, a и b - известные стороны, C - угол между ними.
Для нашей задачи, мы имеем:
a = 2 см,
b = 9 см,
C = 60°.
Подставляя значения в формулу, получим:
c^2 = 2^2 + 9^2 - 2 * 2 * 9 * cos(60°).
Давайте посчитаем каждую часть выражения:
2^2 = 4,
9^2 = 81,
cos(60°) = 0.5.
Теперь заменим значения в исходном уравнении:
c^2 = 4 + 81 - 2 * 2 * 9 * 0.5.
Выполняя вычисления по шагам:
c^2 = 4 + 81 - 2 * 2 * 9 * 0.5,
c^2 = 4 + 81 - 18,
c^2 = 67.
Теперь, чтобы найти третью сторону треугольника c, нам нужно извлечь квадратный корень из обеих сторон уравнения:
c = sqrt(67).
Финальный ответ будет: третья сторона треугольника равна примерно sqrt(67) см.
Надеюсь, я смог подробно и понятно объяснить решение этой задачи. Если остались какие-либо вопросы, пожалуйста, не стесняйтесь задавать их.