В треугольнике ABC ∠C = 90°, AD – биссектриса, ∠A = 60°, AC = 2 см.

а) Решите треугольник ABD ( ).

б) Найдите площадь треугольника ABD ( ).

Ответы

rudens2007 17.02.2022 10:09

а) ∠В = 30°, АВ=4 см, AD=ВD=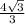 $\frac{4\sqrt{3} }{3}$ см ∠D=120°

б) S = 2√3 cм²

Объяснение:

а) Сумма острых углов прямоугольного треугольника равна 90°

∠В=90°-∠А=90°-60°=30°

Катет прямоугольного треугольника, лежащий напротив угла в 30° равен половине гипотенузы.

⇒ АВ=2*АС=2*2=4см

По теореме Пифагора найдём катет ВС:

$BC=\sqrt{AB^{2}-AC^{2} } =\sqrt{4^{2}-2^{2} } =\sqrt{12} =2\sqrt{3}$

ВС = 2√3 см

Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.

$\dfrac{AB}{BC} =\dfrac{BD}{DC} \\\\\\\dfrac{4}{2} =\dfrac{BD}{2\sqrt{3}-BD } \\\\\\BD=4\sqrt{3} -2BD\\\\3BD=4\sqrt{3} \\\\BD=\dfrac{4\sqrt{3} }{3}$

Рассмотрим ΔABD: ∠ВАD=30° - так как AD – биссектриса, ∠В=30° ⇒ ΔABD- равнобедренный, AD=ВD=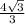 $\frac{4\sqrt{3} }{3}$ см

Так как сумма углов треугольника = 180°, то

∠АDB = 180-∠ВАD-∠В=180-30-30=120°

б) Площадь прямоугольного треугольника равна произведению двух его катетов деленное на 2:

$S = \dfrac{1}{2} *BC*AC=\dfrac{1}{2} *2\sqrt{3} *2=2\sqrt{3}$

S = 2√3 cм²

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

мирок3 24.12.2021 09:37

викуха307 24.12.2021 09:42

1охико1 24.12.2021 09:45

elviraloveelvi 24.12.2021 09:45

1 вариант дайте соч ответ . 8 класс...

hakimjon232 24.12.2021 09:51

Альфа 30° Бетта 45° B 8 см а=?...

lvalerika 24.12.2021 09:52

bolyubash051 24.12.2021 09:53

Жибек20041 03.06.2019 23:40

PORCH1488 03.06.2019 23:40

keke717 06.06.2019 22:30