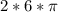В треугольнике ABC, AB = 6, угол C = 30 °. Найдите длину окружности, описанной около треугольника
Другие вопросы по теме Геометрия
Популярные вопросы
- Назовите неопределёную форму всех глаголов из данного . запишите...
2 - Найдите фигуры, для которых будут истинным высказывание: эта фигура-часть...
1 - Решить уравнения: 1). (m-0,67)•0,02=0,0152 2) (y-15,7): 19,2=4,7...
2 - Плюсы и минусы правления юстиниана. и вывод...
1 - Найди значения выражения: 2,1* (6- 0,62)-2,431: 0,26...
3 - Вулкан везувий на апеннинах расположен на высоте 1.277 метров над...
3 - Найти родственные слова, и рядом написать другое родственное слово,...
1 - Put the words in the correct order to mae sentences. 1) bed/never/go/to/we/very...
2 - Is there a beach? yes, there is. are there any supermarkets? no,...
3 - Петя сбегает с 4 этаж на первый на 2 секунды быстрее,чем мама едет...
2
Объяснение:
Начертив треугольник и круг, мы видим, что известный нам угол С лежит напротив известного отрезка AB. Вспоминаем свойства окружности, которая описывает треугольник. "R окружности, описанной около треугольника, равен отношению стороны треугольника к удвоенному синусу противолежащего угла". Короче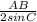
Синус 30 градусов = 1/2. Следовательно, R =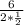 = 6. Далее используем формулу длины окружности и получаем
= 6. Далее используем формулу длины окружности и получаем