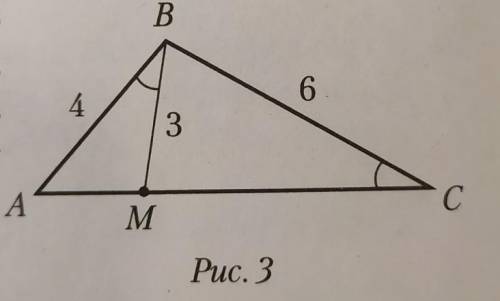
В треугольнике ABC (рис. 3) проведен отрезок ВК так,
что угол ABM = углу C, AB = 4 см,
BM = 3 см, ВС = 6 см. Найди-
те длину стороны АС.
Другие вопросы по теме Геометрия
Популярные вопросы
- 4-тапсырма. Оқшау сөздің қай түрі? 1. Туу, не деген қараңғы-ай!2. Бәлкім,...
1 - Знайдіть суму перших тридцяти членів арифметичної прогресії (an) якщо...
3 - Історичний портрет Октавіана Августа.Будь ласка за цим планом....
2 - с заданием по английскому! Нужно сделать 1-ый лист....
1 - Музыкальная литература, за все!...
3 - Место человека в живой природе ...
2 - Чем питались гунны?история Казахстана ...
1 - всем привет я хочу найти друга (все равно на возраст и пол ) если кому-то...
1 - В основу каких опер легли произведения А.С. Пушкина? 1)Снегурочка 2)Сказка...
3 - Проверти я правильно зделала или нет ?...
3
ответ: Пусть ∠ МВС = Ф, ∠ВМС=ω, ∠А=α, ∠АМВ=β, β+ω=180° как смежные углы и sinβ = sin(180°-ω) = sinω. В ΔАМВ по теореме синусов: sin∠C /АМ = sinω /4, в ΔВМС по т. синусов: sin∠C /3 = sinβ /6 ⇒
3/АМ = 6/4 ⇒ АМ = 2 ⇒ sinω = sinβ = 2*sin∠C
По теореме косинусов для ΔАМВ: АМ² = АВ² + ВМ²- 2*АВ*ВМ*cos∠C ⇒
2² = 4²+3² - 2*4*3*cos∠C ⇒ cos∠C = 21/24 = 7/8 ⇒
sin∠C = (1 - cos²∠C)^1/2 = √15/8, sinω = 2*sin∠C = √15/4, cosω=1/4
Ф = 180° - ω - ∠С ⇒ sin Ф = sin (ω+∠C) = sinω*cos∠C + cosω*sin∠C =
= √15/4 * 7/8 + 1/4 * √15/8 = 8√15/32 = √15/4 = sinω ⇒ по теореме синусов sinФ /МС = sinω /6⇒ МС = 6 ⇒ АС = АМ + МС = 2 + 6 = 8