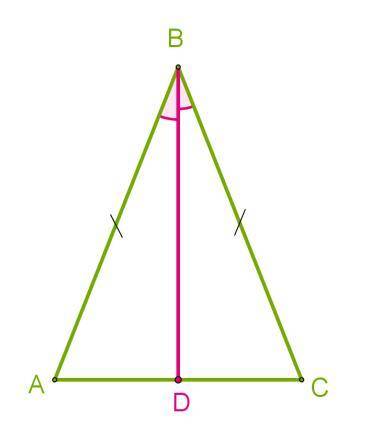
В равнобедренном треугольнике с длиной основания 27 cм проведена биссектриса угла ∡ABC. Используя второй признак равенства треугольников, докажи, что отрезок BD является медианой, и определи длину отрезка AD. Рассмотрим треугольники ΔABD и Δ
(треугольник записать в алфавитном порядке);

1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡ A = ∡
;

2. так как проведена биссектриса, то ∡
= ∡ CBD;

3. стороны AB=CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC —
.

По второму признаку равенства треугольников ΔABD и ΔCBD равны.
Значит, равны все соответствующие элементы, в том числе стороны AD=CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.

AD= см.

Для доказательства того, что отрезок BD является медианой в треугольнике ABC, и определения длины отрезка AD, мы будем использовать второй признак равенства треугольников.

Доказательство:

1. Так как данный треугольник ABC - равнобедренный, то прилежащие к основанию углы А и В равны. Это значит, что ∡А = ∡В.

2. Поскольку проведена биссектриса, то ∡В = ∡CBD.

3. Также мы знаем, что сторона AB = сторона CB в треугольниках ABD и CBD, поскольку треугольник ABC равнобедренный.

Используя второй признак равенства треугольников, мы можем сделать вывод, что треугольники ABD и CBD равны, так как у них равны все соответствующие элементы (согласно пункту 1 и 2).

Значит, стороны AD=CD, и отрезок BD является медианой данного треугольника (так как медиана делит основание пополам).

Теперь нам нужно найти длину отрезка AD.

Из предыдущего пункта видно, что сторона AD=CD.

Поэтому, чтобы найти длину отрезка AD, нам нужно определить длину отрезка CD.

В треугольнике CBD мы уже знаем, что сторона CB равна 27 см (это длина основания данного треугольника).

Для определения длины отрезка CD мы можем воспользоваться теоремой о биссектрисе в треугольнике, которая утверждает, что биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух других сторон треугольника.

Используя данную теорему, мы можем написать следующее уравнение:

CB/CD = AB/AD

Так как стороны AB и CB равны (это свойство равнобедренного треугольника), и стороны AD и CD также равны (это мы только что доказали), мы можем записать уравнение следующим образом:

27/CD = 27/AD

Умножаем обе части уравнения на CD:

27 = 27*CD/AD

Теперь мы можем найти значение отрезка CD, подставив известные значения в уравнение:

27 = 27*CD/AD

Раскрываем скобку:

27*AD = 27*CD

Теперь делим обе части уравнения на 27:

AD = CD

Таким образом, мы получили, что отрезок AD равен отрезку CD.

Итак, ответ: отрезок BD является медианой, и длина отрезка AD равна длине отрезка CD.