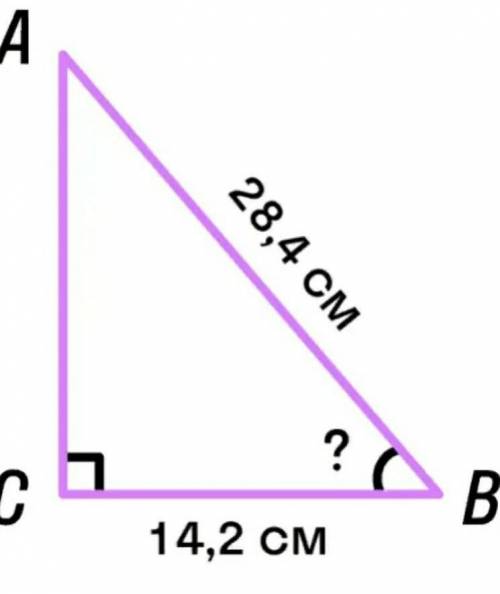
В прямоугольном треугольнике ABC (угол C=90°) сторона BC=14,2 см, а сторона AB=28,4 см. Найди угол B​

ответ: привет

Объяснение:

в тебе math way

Объяснение:

там в телеге или в браузере взломку скачай там все о матеши очень

Для решения этой задачи используем теорему косинусов. Теорема косинусов позволяет нам находить углы или стороны треугольника, если известны длины всех его сторон.

В данной задаче известны длины сторон AB и BC треугольника ABC. Из задания также известно, что угол C является прямым, то есть C = 90°.

Теперь применим теорему косинусов:

cos(B) = (AB^2 + BC^2 - AC^2) / (2 * AB * BC),

где AC - неизвестная сторона треугольника.

Для нахождения угла B нам необходимо найти cos(B) и затем применить обратную функцию косинуса.

1. Найдем длину стороны AC, применив теорему Пифагора:
AC^2 = AB^2 + BC^2,
AC^2 = 28,4^2 + 14,2^2,
AC^2 = 806,56 + 201,64,
AC^2 = 1008,2,
AC ≈ √1008,2,
AC ≈ 31,74 см.

2. Используем найденные значения в формуле cos(B):
cos(B) = (28,4^2 + 14,2^2 - 31,74^2) / (2 * 28,4 * 14,2),
cos(B) = (806,56 + 201,64 - 1008,2) / (2 * 28,4 * 14,2),
cos(B) = 0,00556.

3. Найдем значение угла B, применяя обратную функцию косинуса:
B = arccos(0,00556),
B ≈ 89,94°.

Таким образом, угол B ≈ 89,94°.