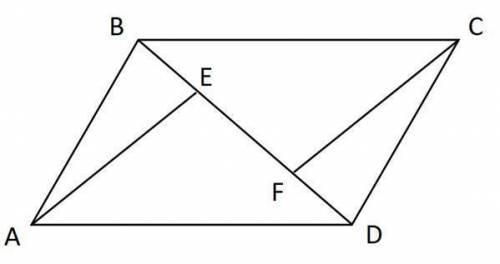
В четырехугольнике ABCD BE=DF, AE||CF, ∠BAD+∠ADC=180°. Докажите, что ABCD – параллелограмм.
Другие вопросы по теме Геометрия
Популярные вопросы
- Complete gaps 1-4 in the review below with suitable phrases from exercise 1...
3 - Параллельные прямые CD и ВЕ пересекают стороны угла AOF. Найдите длину отрезка...
2 - Виконай додавання 13+(-18)...
1 - Дати відповідь на Чи можно назвати повітря насиченим, якщо за температури +10...
2 - Просклоняйте мақал-мәтелдер по падежам....
2 - Задания на фото, первый номер НЕ нужно делать...
3 - Ребята посоветуйте хоррор фильм...
3 - В якому порядку за правилами Excel будуть розміщуватись дані різних типів після...
2 - установіть відповідність :1.ХХ. 2.ХУ. 3.ZZ. 4.ZW. A.Самиця шимпанзе. Б.Самець...
2 - З яких елементів складається Та який заряд має ядро атома Ag...
1
Объяснение:
Дано: ABCD.
BE=DF; AE║CF;
∠BAD+∠ADC=180°.
Доказать: ABCD – параллелограмм.
Доказательство:
1) Если при пересечении двух прямых третьей, сумма односторонних углов равна 180°, прямые параллельны.
∠BAD+∠ADC=180° (условие) - односторонние при АВ и СD и секущей АD.
⇒ АВ ║ СD
2) ∠1=∠2 - накрест лежащие при АЕ║СF и секущей ВD.
∠1=∠3; ∠2=∠4 - вертикальные.
⇒ ∠3=∠4.
3) Рассмотрим ΔАВЕ и ΔFCD.
BE=DF (условие)
∠3=∠4 (п.2)
∠АВЕ=∠FDC - накрест лежащие при АВ║СD и секущей BD.
⇒ ΔАВЕ = ΔFCD (по стороне и прилежащим к ней углам, 2 признак)
⇒АВ = CD (соответственные элементы)
Признак параллелограмма: если в четырехугольнике две противоположные стороны равны и параллельны - это параллелограмм.
АВ ║ СD ; АВ = CD
⇒ ABCD – параллелограмм.