У прямокутному трикутнику АВС ( < С=90°) провели висоту СD. Знайдіть відрізок ВD, якщо АВ=8см, ВС=4см​

ответ: 2 см

Объяснение:

Найдём сначала третью сторону ΔАВС по теореме Пифагора

АС² + ВС² = АВ²

АС²  = АВ² - ВС²

АС² = 8² - 4²

АС² = 64 - 16

АС² = 48

АС = √48 = 4√3

Высота прямоугольного треугольника, опущенная из вершины прямого угла вычисляется по формуле: h =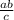 , где а и в - катеты, с - гипотенуза

h =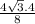 = 2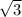

В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом: h =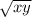 , где х и у  - это отрезки, на которые высота делит гипотенузу.

Пусть BD = х см, тогда АD = (8 - х) см.

Значит, СD =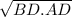

CD² = BD . AD

(2√3)² = х · ( 8 - х )

х² - 8х + 12= 0

х = 2 или х = 6

Условию задачи удовлетворяет х=2 ( проверяем теорему Пифагора для ΔCBD).

ответ : ВD = 2 см.

Значи