Геометрия: S BMN = 4 см^2 Найти площадь !!

S BMN = 4 см^2
Найти площадь !!

S BMN = 4 см^2 Найти площадь !!

Ответы

olesyapetrova8 06.03.2022 10:40

Обозначим BN=x, ∠B=α

AN=BN, поэтому AB=2x

Площадь треугольника равна половине произведения двух сторон и синуса угла между ними.

Площадь ΔBMN:

$S = \frac{1}{2} \times 2x \times \sin( \alpha ) = 4 \\x \sin( \alpha ) = 4 \\ \sin( \alpha ) = \frac{4}{x}$

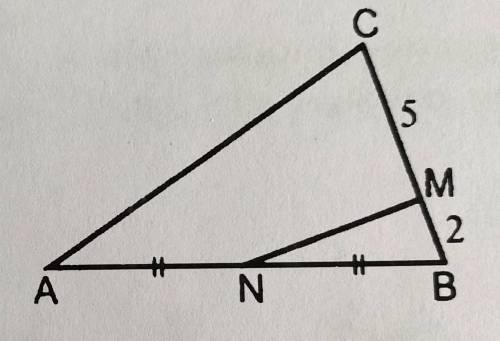
BC=5+2=7

Площадь ABC:

$S = \frac{1}{2} \times 2x \times 7 \times \sin( \alpha )$

Подставляем sin(α)=4/x

$S_{ \triangle} = \frac{1}{2} \times 2x \times 7 \times \frac{4}{x} \\ S_{ \triangle} = 7x \times \frac{4}{x} \\ S_{ \triangle} = 7 \times 4 \\ S_{ \triangle} = 28$

Площадь треугольника ABC 28 см²

ПОКАЗАТЬ ОТВЕТЫ

Рюзаки1 12.01.2024 10:01

Для решения данной задачи нам необходимо определить площадь треугольника BMN.

Для начала, давайте рассмотрим, какие данные у нас уже имеются:

- У нас дано, что площадь треугольника BMN равна 4 см^2 (S BMN = 4 см^2).
- У нас дан рисунок треугольника BMN.

Таким образом, наша задача - найти площадь треугольника BMN.

Шаг 1: Понимание основных понятий
Перед тем, как начать решение задачи, нужно разобраться в основных понятиях, связанных с площадью треугольника.

- Треугольник - это геометрическая фигура, которая состоит из трех сторон и трех углов.
- База треугольника - это одна из сторон треугольника.
- Высота треугольника - это отрезок, проведенный из вершины треугольника к его базе и перпендикулярный базе.

Эти определения помогут нам дальше в решении задачи.

Шаг 2: Определение формулы для нахождения площади треугольника

Существует несколько способов найти площадь треугольника, но мы воспользуемся наиболее простым способом, который основан на базе и высоте треугольника.

Формула для нахождения площади треугольника:
S = (b * h) / 2

где S - площадь треугольника, b - база треугольника, h - высота треугольника.

Шаг 3: Решение задачи

Теперь, когда мы знаем формулу для нахождения площади треугольника, мы можем приступить к решению задачи.

На рисунке дана база треугольника - отрезок BN. Чтобы найти площадь треугольника, нам нужно знать высоту треугольника, проведенную из вершины M к его базе BN.

Однако, у нас нет прямых данных о высоте треугольника. Поэтому нам потребуется найти ее.

Шаг 4: Нахождение высоты треугольника

Мы можем воспользоваться теоремой Пифагора, чтобы найти высоту треугольника.

Теорема Пифагора гласит:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

В нашем случае, треугольник BMN не является прямоугольным. Однако, мы можем дополнить его так, чтобы получить прямоугольный треугольник.

Для этого, мы проведем отрезок MC, который будет перпендикулярным к BN и будет дополнительной высотой треугольника.

Теперь у нас есть прямоугольный треугольник BMC. Применим теорему Пифагора к этому треугольнику.

MC^2 + BM^2 = BC^2

Теперь давайте запишем данные, которые мы знаем:

- MC - дополнительная высота треугольника, которую мы ищем
- BM = 3 см (это следует из рисунка)
- BC = 5 см (это следует из рисунка)

Теперь мы можем приступить к нахождению высоты треугольника при помощи теоремы Пифагора.

MC^2 + 3^2 = 5^2

MC^2 + 9 = 25

MC^2 = 25 - 9

MC^2 = 16

MC = √16

MC = 4

Таким образом, мы нашли высоту треугольника, равную 4 см.

Шаг 5: Нахождение площади треугольника

Теперь, когда у нас есть база (BN) и высота (MC) треугольника, мы можем подставить их в формулу для нахождения площади треугольника.

S = (b * h) / 2

S BMN = (BN * MC) / 2

S BMN = (2 см * 4 см) / 2

S BMN = 8 см^2 / 2

S BMN = 4 см^2

Таким образом, мы опять получили, что площадь треугольника BMN равна 4 см^2, что совпадает с данными, которые мы имели изначально.

Ответ: Площадь треугольника BMN равна 4 см^2.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия