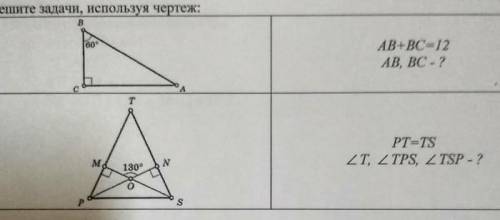
Решите задачи используя чертёж решите ​

1. 4см  и 8 см

2. ∠Т = 50°, ∠ ТPS = ∠TSP = 65°

Объяснение:

1. ВС - катет лежащий напротив угла 30° ⇒ он равен половине АВ по свойству прямоугольного треугольника.

Пусть ВС - х. Тогда АВ - 2х. Составим уравнение:

х+ 2х = 12

3х = 12

х = 4 см.

2х = 8 см.

2. ∠ТPN  = 130 - 90 = 40°, т.к. ∠ MON - внешний по отношению к ΔPMO

∠NPS = (180 - 130)/2 = 25°, т.к. ΔPMS = ΔPNS по гипотенузе и острому углу.

⇒ ∠ ТPS = ∠TSP = ∠ТPN + ∠NPS = 40 + 25 = 65°, т.к. Δ ТPS равнобедренный

∠Т = 180- 65 - 65 = 50°