Решите дано: OA=OC=10. OB=6. AC||OY
найдите координаты векторов OA. OC. AC​

Для того чтобы найти координаты векторов OA, OC и AC, мы должны знать координаты точек O, A и C.

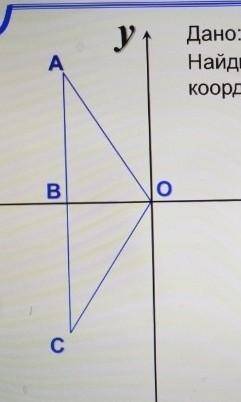
Изображение показывает прямоугольный треугольник OBC, где OB = 6, OA = OC = 10 и AC||OY.

Для начала, давайте определим координаты точки O. Поскольку нам не даны конкретные значения координат, мы можем выбрать любые значения, подходящие для решения этой задачи. Для простоты выберем O(0,0) в качестве начала координат.

Теперь нам нужно найти координаты точек A и C. Поскольку OB = 6, учитывая что O(0,0), мы можем сказать, что B(6,0). Теперь у нас есть начальные координаты O(0,0) и B(6,0).

Также, поскольку OA = OC = 10, мы можем найти координаты точек A и C, используя теорему Пифагора для прямоугольного треугольника OAC. А именно, мы можем использовать формулу:

AC^2 = OA^2 - OC^2.

Подставляя значения, получаем:

AC^2 = 10^2 - 10^2 = 100 - 100 = 0.

Это означает, что AC равен нулю, то есть точки A и C совпадают. Мы можем выбрать любые значения для координат, подходящие для этой ситуации. Для простоты, давайте выберем A(10,0) и C(10,0).

Теперь у нас есть значения координат точек O(0,0), A(10,0) и C(10,0), и мы можем найти векторы OA, OC и AC, используя разницу координат.

Вектор OA = A - O = (10-0,0-0) = (10,0).

Вектор OC = C - O = (10-0,0-0) = (10,0).

Вектор AC = C - A = (10-10,0-0) = (0,0).

Итак, координаты векторов OA, OC и AC равны:

OA: (10,0).

OC: (10,0).

AC: (0,0).