решить задачу номер 8. (По теореме о трех перпендикулярах)

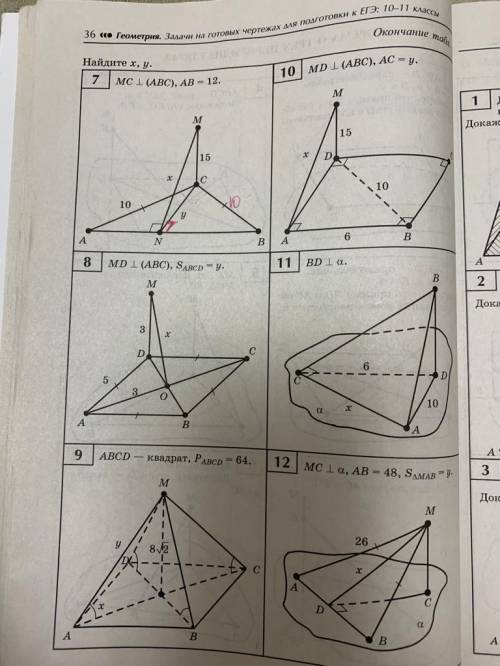
MD⊥(АВС) , AB=BC=CD=AD , AD=5,AO=3,MD=3. Найти площадь ABCD ,  расстояние от точки М до точки О

Объяснение:

1) Все стороны АВСD  равны , значит это ромб . Диагонали ромба взаимно-перпендикулярно⇒ ∠АОВ=90°.

ΔАОВ- прямоугольный , по т Пифагора ,

ОВ=√(АВ²-АО²)=√(5²-3²)=4 (ед).

2) Диагонали ромба точкой пересечения делятся пополам , поэтому ВD=8 ед , АС=6 см.

S( ромба )=1/2*d₁*d₂ ,  S( ромба )=1/2*8*6=24 (ед²).

3) Тк МD⊥ (ABC) , то  MD⊥DO .

ΔMDО прямоугольный , по т Пифагора ,

МО=√(MD²+DО²)=√(3²+4²)=5 (ед).