Решение прямоугольных треугольников.
Найти x и y.
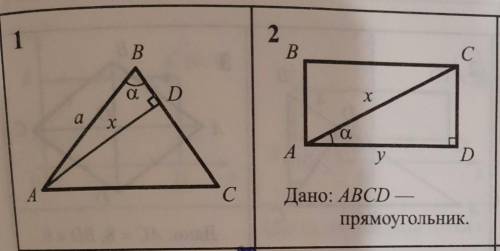
Другие вопросы по теме Геометрия
Популярные вопросы
- Сравнительный анализ восстания сырыма датова (датулы) и емельяна пугачева. ! 70...
1 - Укажите вещества из 4оторых состоят следующие тела: ножницы, стакан,карандаш, ложка,...
3 - Сравнительный анализ личностей сырыма датова (датулы) и емельяна пугачева!...
1 - Найдите столярное произведение векторов a(5; 7) b (15; 4) какой угол между ними?...
1 - Кто ввел даойные латинские названия род и вид...
1 - Заполните таблицунаправление живописиназвание посвящённых картин жан-поль марат...
2 - Вершина лопасти вентилятора с радиусом ,равным 20 см, вращается с линейной скоростью...
2 - Задайте вопросы к выделенным словам добавляя: . ❗❗❗...
1 - На рисунке изображён план торгового центра сторона каждой клетки на плане равна...
2 - Проверить бинарное отношение на рефлексивность, симметричность и транзитивностьr={...
2
Для начала, вспомним основные свойства прямоугольных треугольников. Прямоугольный треугольник определяется наличием одного прямого угла (угол, равный 90 градусам). В таком треугольнике, сторона, противолежащая прямому углу, называется гипотенузой. Остальные две стороны называются катетами.
В заданном треугольнике нам даны два катета: x и y.
Чтобы решить эту задачу, мы можем использовать одну из основных теорем прямоугольных треугольников - теорему Пифагора. Согласно этой теореме, сумма квадратов катетов равна квадрату гипотенузы. Формула для этой теоремы выглядит следующим образом: a^2 + b^2 = c^2, где a и b - катеты, а c - гипотенуза.
Применяя теорему Пифагора к нашей задаче, мы можем записать уравнение следующим образом:
x^2 + y^2 = 13^2.
Теперь мы можем приступить к решению этого уравнения. Для этого разрешимо выразим одну из переменных через другую. Для примера, давайте выразим y через x:
y^2 = 13^2 - x^2.
Теперь, чтобы найти значение переменных x и y, нам необходимо одновременно решить два уравнения:
y = √(13^2 - x^2) (выражение для y, полученное из теоремы Пифагора)
и
x + y = 15 (условие задачи, по которому сумма сторон должна быть равна 15).
Подставляя первое уравнение во второе, мы получим:
x + √(13^2 - x^2) = 15.
Для решения этого уравнения нам следует проделать несколько шагов:
1. Возвести оба выражения уравнения в квадрат (это удалит корень):
(x + √(13^2 - x^2))^2 = 15^2.
2. Раскрыть скобку, используя формулу (a + b)^2 = a^2 + 2ab + b^2:
x^2 + 2x√(13^2 - x^2) + (13^2 - x^2) = 225.
3. Объединить подобные слагаемые:
x^2 + 2x√(13^2 - x^2) + 169 - x^2 = 225.
4. Упростить уравнение, отменяя подобные слагаемые:
2x√(13^2 - x^2) = 225 - 169.
5. Вычислить правую часть уравнения:
2x√(13^2 - x^2) = 56.
6. Разделить обе части уравнения на 2:
x√(13^2 - x^2) = 28.
7. Возведем обе части уравнения в квадрат:
x^2(13^2 - x^2) = 28^2.
8. Раскроем скобки:
13^2x^2 - x^4 = 784.
9. Переставим слагаемые в порядке убывания степени:
x^4 - 13^2x^2 + 784 = 0.
Теперь это уравнение является квадратным. Для его решения мы можем воспользоваться квадратной формулой:
x = (-b ± √(b^2 - 4ac))/(2a).
В нашем случае, a = 1, b = -13^2 и c = 784.
Подставив эти значения в формулу, мы можем найти значения для x. После нахождения x, мы можем подставить его в одно из уравнений (x + y = 15) для нахождения соответствующего значения y.
Надеюсь, это подробное пошаговое решение поможет вам понять, как найти значения x и y в данной задаче. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать их.