Впрямоугольном треугольнике один из углов 30 градусов и меньше катет имеет длину 6 см.
найти длину высоты треугольника, проведенную к гипотенузе.

Question

Геометрия: Впрямоугольном треугольнике один из углов 30 градусов и меньше катет имеет длину 6 см. найти длину высоты треугольника, проведенную к гипотенузе.

Wenros · Answer

Меньший катет как раз лежит напротив 30 градусного угла. Он и равен половине гипотенузы, сама гипотенуза равна 12.

$cos30 = \frac{\sqrt{3} }{2}$

Неизвестный катет равен произведению гипотенузы на косинус этого угла, т.е.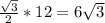 $\frac{\sqrt{3} }{2}*12=6\sqrt{3}$

Распишем площадь треугольника двумя как половина произведения катетов и как половина произведения основания (гипотенузы) и высоты (проведенной к гипотенузе)

$0.5*6\sqrt{3}*6=0.5*h*12;\\ 36\sqrt{3} =12h; \\ h=3\sqrt{3}$