Два круга касаются снаружи в точке а. найти длину их общей внешней касательной и расстояние от точки а к общей внешней

Question

Геометрия: Два круга касаются снаружи в точке а. найти длину их общей внешней касательной и расстояние от точки а к общей внешней касательной, если радиусы кругов 2 см и 8 см.

dbb26444 · Answer

Рисунок прилагается. Таких внешних касательных существует всего две. Они пересекаются в точке G. BD и CF - радиусы, перпендикулярные касательной GE. Треугольники GDB и GFC подобны по двум углам (G - общий угол, а также ∠GBD=∠GFC=90° (как раз эти самые радиусы)

Тогда из подобия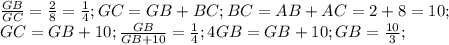 $\frac{GB}{GC} =\frac{2}{8} =\frac{1}{4} ; GC = GB + BC; BC = AB + AC =2 + 8 = 10;\\ GC = GB + 10; \frac{GB}{GB+10}=\frac{1}{4};4GB=GB+10;GB=\frac{10}{3};$

Наше искомое расстояние AP. Это заодно значит, что AP перпендикулярно GT (второй касательной, можно было так же начертить и с первой, это не принципиально). Тогда треугольники GBH и GAP тоже подобны по двум углам (G - общий и ∠GHB=∠GPA=90°)

и значит, что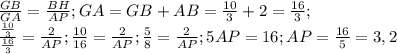 $\frac{GB}{GA} =\frac{BH}{AP} ; GA = GB + AB=\frac{10}{3}+2=\frac{16}{3};\\ \frac{\frac{10}{3} }{\frac{16}{3} }=\frac{2}{AP};\frac{10}{16}=\frac{2}{AP};\frac{5}{8}=\frac{2}{AP};5AP=16; AP=\frac{16}{5}=3,2$

ответ: 3,2 см.

Два круга касаются снаружи в точке а. найти длину их общей внешней касательной и расстояние от точки

Два круга касаются снаружи в точке а. найти длину их общей внешней касательной и расстояние от точки а к общей внешней касательной, если радиусы кругов 2 см и 8 см.

Популярные вопросы