Правильный треугольник со стороной 6 см вписан в окружность. найти периметр шестиугольника описанного около этой окружности
Ответы
Окружность является описанной около треугольника и вписанной в шестиугольник. Найдем радиус этой окружности по формуле описанной около правильного треугольника окружности: 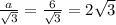 см. Сторону шестиугольника можно найти по формуле вписанной в правильный шестиугольник окружности:
см. Сторону шестиугольника можно найти по формуле вписанной в правильный шестиугольник окружности: 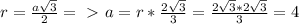 см. Значит, периметр шестиугольника равен: 6*4 = 24 см.
см. Значит, периметр шестиугольника равен: 6*4 = 24 см.
ПОКАЗАТЬ ОТВЕТЫ
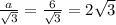 см. Сторону шестиугольника можно найти по формуле вписанной в правильный шестиугольник окружности:
см. Сторону шестиугольника можно найти по формуле вписанной в правильный шестиугольник окружности: 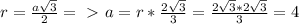 см. Значит, периметр шестиугольника равен: 6*4 = 24 см.
см. Значит, периметр шестиугольника равен: 6*4 = 24 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Посмотри в справочнике, что означают слова керамика, фарфор, бетон...
3 - Почему гранит применяют в строительстве часто, а каменную соль лишь...
3 - Расскажи, что делают из фарфора, керамики. Где используют бетон,...
3 - Приведи примеры источников звука...
2 - Как ты думаешь, чем музыка отличается от шума?...
3 - Определить отпускную и оптово-отпускную цену телевизора. Прямые...
2 - Какую музыку ты любишь? Есть ли у тебя любимые музыкальные произведения?...
1 - Когда фея подарила Золушке бальное платье, девушке, конечно, захотелось...
1 - Назови эти музыкальные инструменты. Знаешь ли ты, как они звучат?...
3 - Вспомни звуки твоего дома. Какие звуки ты слышишь утром, днём, вечером?...
1