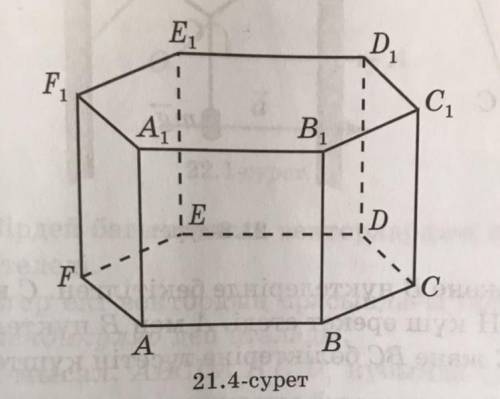
правильной шестиугольной призме через векторы АВ, AF и АA1, выразите следующий вектор: a) AD1; б) AC1, (рис.21.4).
ответ есть,но нужно подробное решение.

Для решения этой задачи, нам понадобится знание о свойствах шестиугольных призм и векторной алгебры.

По определению шестиугольной призмы, ее боковая грань является правильным шестиугольником, а основаниями служат две плоскости, параллельные друг другу и правильные шестиугольники.

Мы также знаем, что векторы AB, AF и AA1 образуют систему координат в пространстве, где AB является осью X, AF - осью Y, а AA1 - осью Z.

Для выражения вектора AD1 мы можем использовать свойство параллельных прямых в пространстве. Поскольку AD1 параллелен AB, то их векторы будут коллинеарными, то есть их координаты будут пропорциональны.

Предположим, что вектор AD1 имеет координаты (x, y, z). Тогда вектор AB имеет координаты (1, 0, 0) (так как AB является осью X), и мы можем записать:

(x/1) = (y/0) = (z/0)

Очевидно, что оба отношения y/0 и z/0 не имеют смысла, поскольку мы не можем делить на ноль. Координата x может быть какой угодно, так как это не влияет на коллинеарность векторов. Таким образом, мы можем сказать, что вектор AD1 имеет координаты (x, 0, 0), где x - это произвольная константа.

Ответ для вектора AD1 - (x, 0, 0).

Теперь рассмотрим вектор AC1. По определению шестиугольной призмы, векторы AB, AF и AA1 образуют систему координат, где AB - ось X, AF - ось Y и AA1 - ось Z. Таким образом, мы можем сказать, что вектор AC1 будет иметь координаты (0, 0, z), где z - это произвольная константа.

Ответ для вектора AC1 - (0, 0, z).

Итак, чтобы выразить векторы AD1 и AC1, мы использовали свойства параллельных прямых в пространстве и знания о системе координат шестиугольной призмы.

Надеюсь, это решение поможет вам понять, как выразить данные векторы в данной задаче. Если у вас возникнут еще вопросы, не стесняйтесь задавать их.