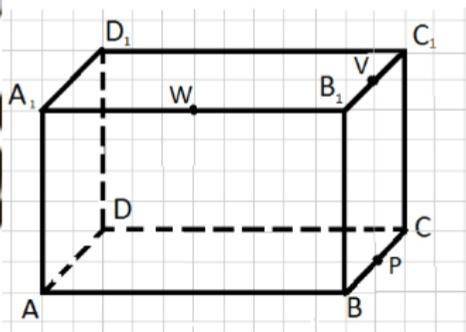
построить сечение плоскостью, проходящей через 3 точки

Чтобы построить сечение плоскостью, проходящей через 3 точки, нам понадобится некоторое предварительное знание о плоскостях и их сечениях.

Плоскость - это двумерная геометрическая фигура, которая распространяется бесконечно во всех направлениях. Одна плоскость может пересекать другую плоскость, образуя линию, которая называется сечением.

В данной задаче у нас есть три точки: A, B и C. Нашей задачей является построение плоскости, проходящей через все три эти точки.

Шаг 1: Найдите нормаль к плоскости
Для начала нужно определить вектор нормали к плоскости, чтобы знать, как она ориентирована в пространстве. Для этого можно использовать кросс-произведение векторов.
Возьмем векторы AB и AC. Кросс-произведение этих векторов даст нам вектор, перпендикулярный плоскости. Давайте выполним это вычисление:
AB = B - A = (-3, 1, 1) - (1, -2, 4) = (-4, 3, -3)
AC = C - A = (2, 3, -1) - (1, -2, 4) = (1, 5, -5)

Теперь выполним кросс-произведение:
n = AB x AC = (-4, 3, -3) x (1, 5, -5)

Для вычисления кросс-произведения вычисляем 3 координаты:
n₁ = 3 * (-5) - (-3) * 5 = -15 - (-15) = 0
n₂ = (-4) * (-5) - (-3) * 1 = 20 - (-3) = 23
n₃ = (-4) * 5 - 3 * 1 = -20 - 3 = -23

Таким образом, вектор нормали к плоскости равен (0, 23, -23).

Шаг 2: Уравнение плоскости
Теперь, имея нормаль к плоскости, мы можем записать уравнение плоскости в общем виде, используя одну из точек (скажем, A):
Ax + By + Cz + D = 0

Мы знаем, что координаты точки A равны (1, -2, 4), и нормаль вектора равна (0, 23, -23). Заменим эти значения в уравнении:
0 * x + 23 * y - 23 * z + D = 0

Мы можем решить это уравнение относительно D:
23y - 23z + D = 0
D = -23y + 23z

Таким образом, уравнение плоскости будет иметь вид:
23y - 23z - 23 = 0

Шаг 3: Построение сечения
Теперь мы можем построить сечение плоскостью, проходящей через 3 точки. Выберем два из трех предложенных вариантов точек: A и B.

Подставим координаты точек A и B в уравнение плоскости и решим полученную систему уравнений:

1) Для точки A (1, -2, 4):
23 * (-2) - 23 * 4 - 23 = 0
-46 - 92 - 23 = 0
-161 = 0

2) Для точки B (-3, 1, 1):
23 * 1 - 23 * 1 - 23 = 0
23 - 23 - 23 = 0
0 = 0

Кажется, у нас возникло противоречие. Уравнение 0 = 0 всегда истинно, поэтому получается, что линия сечения будет вырожденной и будет совпадать со всей плоскостью.

В данном случае, сечение просто будет точкой, которая имеет координаты (1, -2, 4).

Таким образом, плоскость, проходящая через все три точки, определяет линию сечения, которая, в данном случае, вырождена и совпадает с точкой (1, -2, 4).