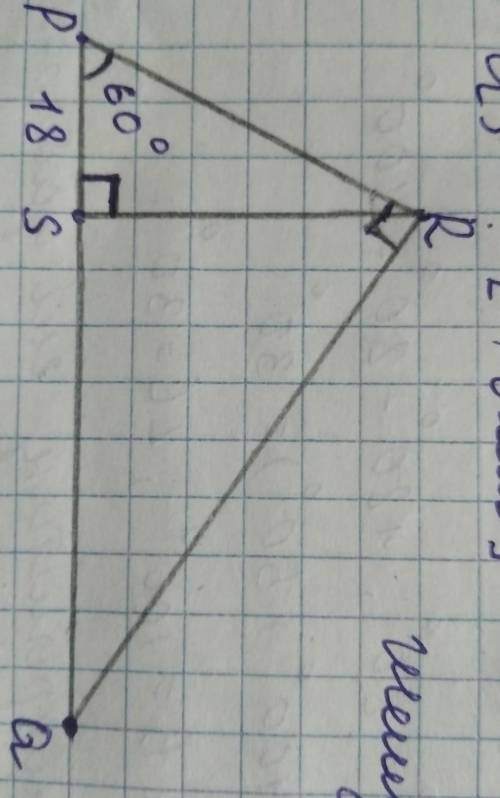
Найдите QS- ?cm
треугольник PQR
<P=60°,<S=90°
PS=18 cm​

Чтобы решить задачу, мы можем использовать теорему косинусов. Она гласит:

c^2 = a^2 + b^2 - 2ab*cos(C)

Где c - длина стороны противолежащей углу C, a и b - длины двух других сторон треугольника, C - угол между этими сторонами.

В нашей задаче у нас есть два угла и сторона между ними. Мы хотим найти длину стороны QS, которую мы обозначим как x.

Из заданных данных мы знаем:

Угол

Угол Сторона PS = 18 см

Нам нужно найти сторону QS. Давайте обозначим сторону PQ как a и сторону QR как b. Таким образом, сторона QS будет являться стороной a.

Теперь применим теорему косинусов к треугольнику PQR.

PS^2 = PQ^2 + QR^2 - 2*PQ*QR*cos(
PS^2 = a^2 + b^2 - 2ab*cos(
Так как у нас угол

PS^2 = a^2 + b^2 - 2ab*cos(30°)

Также нам дано, что PS = 18 см. Подставим эту информацию в уравнение:

18^2 = a^2 + b^2 - 2ab*cos(30°)

324 = a^2 + b^2 - 2ab*cos(30°)

Для удобства найдем cos(30°). Мы знаем, что cos(30°) = √3/2.

324 = a^2 + b^2 - 2ab * √3/2

Данное уравнение может быть решено разными способами. Но чтобы найти конкретную длину стороны QS, нам нужно знать значения a и b. Если у нас были бы эти значения, мы могли бы решить это уравнение относительно x.

Если у вас есть дополнительные данные о треугольнике или вы знаете значения a и b, пожалуйста, укажите это, и я смогу посчитать и продемонстрировать шаги, чтобы найти длину стороны QS.