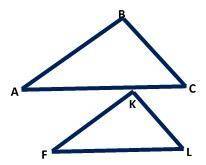
На рисунке представлены два подобных треугольника. Угол C первого равен углу L второго и составляет 650. Сторона AC первого 19,5 см, а сторона FL второго равна 13,0 см. При этом сторона BC первого = 12,0 см, а сторона FK второго = 12,0 см. Найдите длины стороны AB первого и KL второго.
Другие вопросы по теме Геометрия
Популярные вопросы
- Как решить пример 5/6умножить на 5/6...
1 - Складіть рівняння реакції добування натрій гідроксиду за реакції...
2 - Измерьте длину своего шланга? ( как понять это можно? ) пож, вот...
1 - Носительница гемофилии вышла замуж за здорового мужчину ,какие...
3 - Знайдіть радіус кола, описаного навколо правильного шестикутника...
3 - Какое стихотворение великобритании является самым древним? и о...
3 - Автомобіль, що рушає з місця, на першому етапі руху набиає швидкості...
3 - Отражение окружающего мира в художественных образах заключает в...
1 - Решите номер через пропорцию а)x\9=5\9 б)5\x=0.2\3 в)6x\5=18\7...
2 - Составить кроссворд на тему векторы 20 слов...
2
По условию задачи, дано что треугольники ABC и FLK подобны. Это означает, что соответствующие углы треугольников равны и соответствующие стороны пропорциональны.
Так как угол C первого треугольника равен углу L второго треугольника и составляет 650, то угол A первого треугольника равен углу K второго треугольника и составляет 650. То есть, угол A первого треугольника равен 650.
Для нахождения длины стороны AB первого треугольника, будем использовать соответствующую пропорцию между сторонами двух треугольников.
Запишем пропорцию:
AB/FL = AC/FK
Подставляем известные значения:
AB/13 = 19.5/12
Умножаем обе части пропорции на 13:
AB = 13 * 19.5 / 12
AB = 167.5 / 12
AB ≈ 13.96
Таким образом, длина стороны AB первого треугольника примерно равна 13.96 см.
Теперь найдем длину стороны KL второго треугольника, используя ту же пропорцию, но с другими значениями.
Запишем пропорцию:
KL/12 = 13/19.5
Умножаем обе части пропорции на 12:
KL = 12 * 13 / 19.5
KL = 156 / 19.5
KL ≈ 8
Таким образом, длина стороны KL второго треугольника примерно равна 8 см.