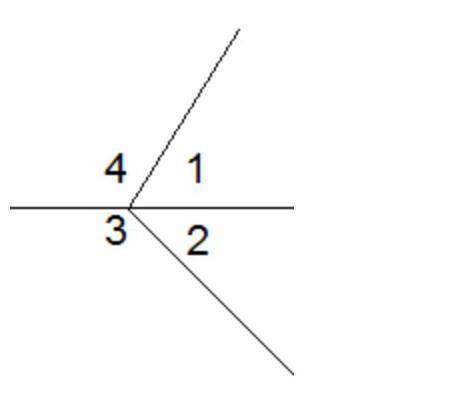
Какое из данных верно
180°=/_1+/_2+/_3+/_4.
180°=/_1+/_3.
/_1+/_2=/_3+/_4
180°=/_2+/_3​

Для решения этой задачи, нам нужно использовать знания о сумме углов треугольника и свойствах равнобедренности.

Первое утверждение говорит, что 180° равно сумме углов 1, 2, 3 и 4. Но у нас нет информации о том, что эти углы составляют треугольник или какие-то другие геометрические фигуры. Так что это утверждение неверно.

Второе утверждение говорит, что 180° равно сумме углов 1 и 3. Но по диаграмме видно, что углы 1 и 3 образуют одну линию, и сумма углов на одной линии равна 180°. Так что это утверждение верно.

Третье утверждение говорит, что сумма углов 1 и 2 равна сумме углов 3 и 4. Но по диаграмме видно, что углы 3 и 4 образуют одну линию, а углы 1 и 2 образуют другую линию, поэтому эти две пары углов не могут быть равны. Так что это утверждение неверно.

Четвертое утверждение говорит, что 180° равно сумме углов 2 и 3. По диаграмме видно, что углы 2 и 3 образуют одну линию, и сумма углов на одной линии равна 180°. Так что это утверждение верно.

Итак, верные утверждения из предложенных это:
180°=/_1+/_3 и 180°=/_2+/_3