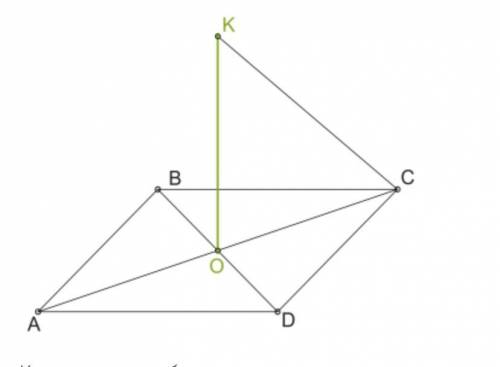
К плоскости ромба проведена перпендикулярная прямая KO через точку пересечения диагоналей. Точка K соединена с вершиной C. Докажи, что BD ⊥ KC.

, уже полтора часа над этой задачей бьюсь.

Для решения этой задачи, нам понадобятся некоторые свойства ромба и прямых на плоскости.

Свойства ромба:
1. Диагонали ромба перпендикулярны.
2. Диагонали ромба делят его на 4 равных треугольника.

Мы можем использовать эти свойства, чтобы решить задачу.

Для начала, обратим внимание на диагонали ромба. Пусть AC и BD - диагонали.

По свойству 1, мы знаем, что AC и BD перпендикулярны.

Теперь, мы проводим перпендикулярную прямую KO к плоскости ромба через точку пересечения диагоналей. Точка K соединена с вершиной C.

Поскольку AC и BD перпендикулярны, а KO - перпендикулярная прямая к плоскости ромба, то KO также перпендикулярна BD (так как они обе перпендикулярны к AC).

Теперь, все, что нам нужно сделать, это доказать, что BD перпендикулярна KC.

Для этого, давайте обратим внимание на треугольники KBC и KDB.

Мы знаем, что точка K соединена с вершиной C и точкой пересечения диагоналей. Поэтому у нас есть горизонтальная сторона KB и вертикальная сторона KC.

Также у нас есть сторона BD. Мы должны доказать, что угол между сторонами BD и KC составляет 90 градусов.

Для этого, давайте взглянем на свойство 2 ромба. Мы знаем, что диагонали ромба делят его на 4 равных треугольника.

Треугольник KBC - один из таких треугольников. Более того, KB и KC являются его сторонами.

Теперь, если у нас есть ромб с вершиной K и диагональю KB, то угол между сторонами KB и KC (в треугольнике KBC) должен быть 90 градусов (так как KB является диагональю ромба и диагонали ромба перпендикулярны).

Таким образом, мы доказали, что в треугольнике KBC угол между сторонами BD и KC равен 90 градусов.

То есть BD перпендикулярна KC.

Надеюсь, это объяснение помогло вам понять решение задачи. Если у вас возникли еще вопросы, пожалуйста, не стесняйтесь задавать их.