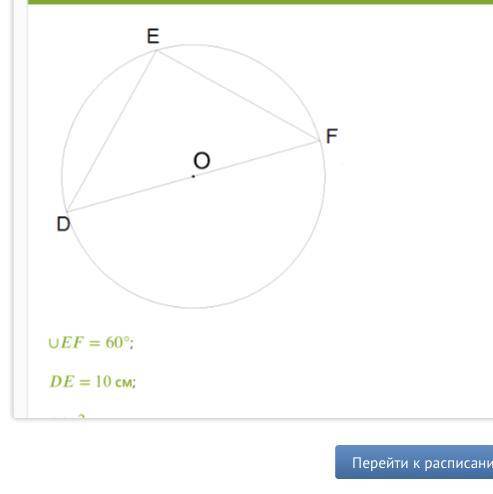
EF=60°; DE=10 см;

п = 3.

Найди длину окружности

С = см

(результат округли до десятых!)

Для решения данной задачи мы можем использовать формулу для длины окружности: С = 2πr, где С - длина окружности, π - число Пи (приближенное значение равно 3.14), r - радиус окружности.

В данном случае, нам не дано значение радиуса окружности. Однако, мы можем найти его, используя сведения из задачи и свойства треугольника.

Из задачи нам дано, что EF = 60° и DE = 10 см. Мы видим, что EF является хордой окружности, проходящей через середину DE.

Так как EF является хордой, а AD и BE являются радиусами, то DE будет являться диаметром окружности. Поэтому, радиус можно найти, разделив диаметр на 2: r = DE/2 = 10/2 = 5 см.

Теперь, имея значение радиуса, мы можем вычислить длину окружности, подставив его в формулу: С = 2πr = 2 * 3.14 * 5 = 31.4 см.

Однако, мы должны округлить результат до десятых, как указано в задаче. Так как следующая цифра после десятых (запятой) равна 4, то округляем значение до 31.4 см.