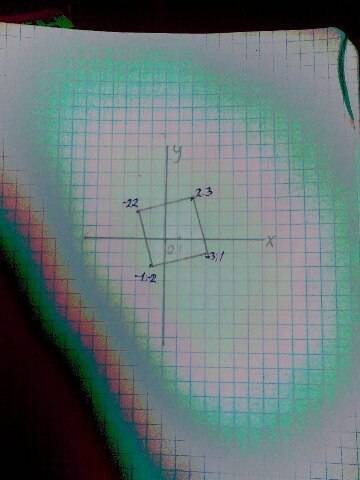
Докажите что четырехугольник abcd с вершинами в точках a(3; -1),b(2; 3),c(-2; 2),d(-1; -2) является прямоугольником.
Ответы
Найдем координаты середин диагоналей четырехугольника: середины ac х=(3-2)/2=0.5 y=(-1+2)/2=0.5 (0.5;0.5) середины BD х=(2-1)/2=0.5 y=(3-2)/2=0.5 Таким образом диагонали четырехугольника пересекаются в точке, что делит их пополам, поэтому за признаком парарлеллограмма четырехугольник АВСD - парареллограмм. Найдем длины диагоналей AC=((-2-3)^2+(-1-2))^2=(-5)^2+(-3)^2=25+9=34 BD=((2+1)^2+(3+2))^2=9+25=34 Диагонали параллелограма ABCD равны АC=BD, за признаком прямоугольника ABCD- прямоугольник. Доказано
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Административно-правовое регулирование общественных отношениосуществляется:а)...
1 - 1.Откуда берётся энергия для синтеза АТФ из АДФ? (с уравнение...
2 - Висота прямоіі призми - ромб, с діагоналями 10 см і 24 см. Меньша...
3 - БІОЛОГІЯ1) прочитати параграф 49;2) виконати завдання: дописати...
3 - Найдите периметр и площадь прямоугольника , если его длина в...
1 - ОЧЕНЬ Дан правильный многоугольник и длина радиуса R окружности,...
1 - За 4 кг яблок заплатили 24 грн. сколько стоит 6,5 кг таких яблок?...
3 - Побудуй прямокутник, площа якого 21 см2, а довжина 7 см...
1 - Очень хотя бы с одним заданием...(...
3 - ответьте на во В каком направлении устанавливается катушка с...
1