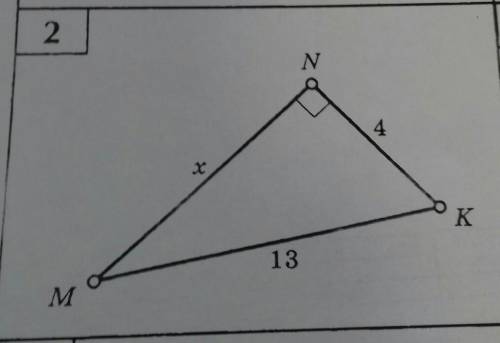
Дано: MNK-треугольгик MK=13,NK=4 Найти MN=x
​

3√17

Объяснение:

∆MNK- прямоугольный треугольник

MK- гипотенуза.

MN- катет

NK- катет.

По теореме Пифагора найдем катет

MN²=МК²-NK²=13²-4²=169-16=153

MN=√153=3√17

Для решения данной задачи воспользуемся теоремой Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

В данном случае треугольник MKN - не прямоугольный, поэтому нам нужно использовать другую формулу, связывающую длины отрезков в треугольнике.

Для треугольников с одинаковыми углами справедливо соотношение длин сторон, которое называется подобием треугольников. Оно утверждает, что отношение длин соответствующих сторон треугольников равно.

В данном случае мы знаем, что отрезок NK равен 4, а отрезок MK равен 13. Также нам известно, что искомый отрезок MN является гипотенузой треугольника MKN.

Согласно теореме Пифагора, в прямоугольном треугольнике с гипотенузой MN и катетами MK и NK выполняется соотношение:
MN^2 = MK^2 + NK^2.

Подставим известные значения:
MN^2 = 13^2 + 4^2.

Вычислим значения в правой части уравнения:
MN^2 = 169 + 16.

MN^2 = 185.

Чтобы найти значение MN, возьмем квадратный корень из обеих частей уравнения:
MN = √185.

Для вычисления квадратного корня из 185 можно воспользоваться калькулятором. Получим приближенное значение:
MN ≈ 13.60.

Таким образом, длина отрезка MN примерно равна 13.60.


В итоге, искомая длина отрезка MN составляет приблизительно 13,60 единиц.